Recordando que un arreglo (en Python llamado lista) es una colección de elementos, como números o cadenas, que están almacenados en un solo contenedor. Este contenedor mantiene todos esos elementos en un orden determinado. Puedes acceder a estos elementos utilizando un índice. En Python, una lista puede contener cualquier tipo de dato, y los elementos dentro de la lista pueden ser modificados.

Cuando pasamos un arreglo como parámetro a una función, lo que realmente estamos haciendo es pasar una referencia al arreglo, no una copia completa del mismo. Esto es importante porque significa que cualquier cambio realizado dentro de la función afectará directamente al arreglo original fuera de la función.

En lugar de pasar una copia del arreglo, en Python, cuando pasamos un arreglo como parámetro, pasamos su referencia. Una referencia es simplemente una dirección de memoria que apunta al arreglo original. Así, cuando modificamos el arreglo dentro de la función, estamos modificando directamente el arreglo que está fuera de la función.

• Ahorro de memoria: Al pasar una referencia en lugar de una copia, evitamos usar memoria adicional para almacenar una copia del arreglo. Esto es muy útil cuando trabajamos con arreglos grandes, ya que puede ahorrar una cantidad significativa de memoria.
• Eficiencia: Al no crear una copia del arreglo, la función puede modificar el arreglo original directamente, lo que puede hacer que el programa sea más eficiente, ya que no se necesita hacer copias adicionales.

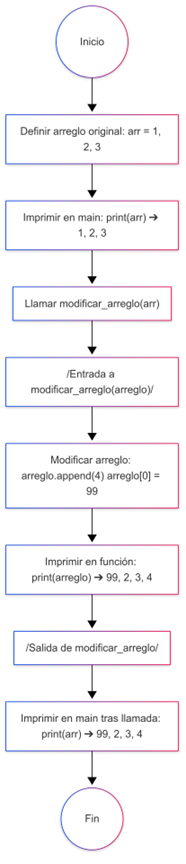
Figura 1: Diagrama de flujo para el paso de arreglos como parámetros Fuente: Creación de autor, D. Nicolalde.

×

Descripción: Este diagrama ilustra cómo los arreglos se pasan como parámetros a una función y cómo los cambios en el arreglo dentro de la función afectan el arreglo original.

Definimos una lista y pasamos esa lista a una función que modificará sus elementos:

                        
def agregar_elemento(lista):
    lista.append(100)

mi_lista = [1, 2, 3]
agregar_elemento(mi_lista)
print(mi_lista)  # Imprime [1, 2, 3, 100]

                        
                    

• Antes de la llamada a la función: mi_lista contiene [1, 2, 3].
• Dentro de la función: Se agrega el número 100 al final de la lista.
• Después de la llamada a la función: El valor de mi_lista es [1, 2, 3, 100], lo que demuestra que la lista fue modificada directamente.

En este caso, vamos a pasar un arreglo de calificaciones de estudiantes para realizar una operación (calcular la media) y modificarlo dentro de la función.

                        
 def calcular_promedio(calificaciones):
    total = sum(calificaciones)
    promedio = total / len(calificaciones)
    return promedio

calificaciones_estudiante = [9, 8, 7, 10, 6]
promedio = calcular_promedio(calificaciones_estudiante)
print(f"El promedio es: {promedio}")  # Imprime el promedio calculado

                        
                    

• Dentro de la función: Se calcula el promedio de las calificaciones pasando la lista a la función.
• Resultado: La función devuelve el valor del promedio que se calcula a partir de los valores en el arreglo.

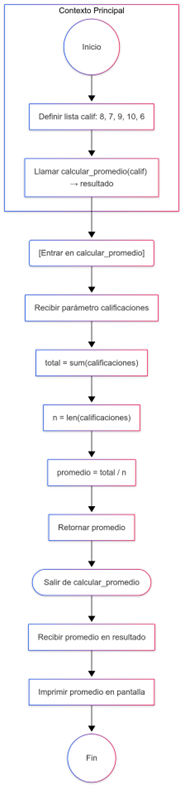
Figura 2: Diagrama de flujo para el paso de un arreglo de calificaciones Fuente: Creación de autor, D. Nicolalde.

×

Descripción: Este diagrama muestra cómo una lista de calificaciones se pasa a la función para realizar un cálculo y luego devolver el resultado.

Ahora, vamos a trabajar con una lista de matrices (listas dentro de listas) y modificarla mediante una función. Esto es útil cuando se tienen arreglos multidimensionales (como matrices).

                        
def modificar_matriz(matriz):
    for i in range(len(matriz)):
        for j in range(len(matriz[i])):
            matriz[i][j] += 1

matriz = [[1, 2, 3], [4, 5, 6]]
modificar_matriz(matriz)
print(matriz)  # Imprime [[2, 3, 4], [5, 6, 7]]

                        
                    

• La función recorre cada elemento de la matriz y le suma 1.
• Modificación: Se modifica directamente el contenido de la matriz porque los arreglos son mutables en Python.

Una función recursiva es una función que se llama a sí misma durante su ejecución. Este tipo de función es especialmente útil cuando necesitamos resolver un problema que puede ser dividido en subproblemas más pequeños y similares entre sí. Es decir, podemos resolver el problema completo repitiendo la misma lógica, pero con datos más simples cada vez.

Las funciones recursivas son muy comunes en problemas de programación que siguen una estructura jerárquica o de árbol, como el cálculo de factoriales, el recorrido de estructuras de datos como árboles y gráficos, y la resolución de problemas matemáticos complejos.

Las funciones recursivas trabajan de una manera especial. Tienen dos componentes esenciales para funcionar correctamente:

1. El Caso Base: El caso base es una condición que detiene las llamadas recursivas. Sin un caso base, la función seguiría llamándose a sí misma de manera infinita, lo que causaría un desbordamiento de pila (stack overflow). El caso base es generalmente una condición simple y directa que resuelve el problema de manera inmediata.
2. La Llamada Recursiva: La función se llama a sí misma con un conjunto más pequeño de datos o una versión más simple del problema. Esto divide el problema original en subproblemas más manejables, y la función sigue llamándose hasta llegar al caso base.

                        
def funcion_recursiva(parametro):
    if parametro <= 0:  # Caso base
        return 0
    else:
        return parametro + funcion_recursiva(parametro - 1)  # Llamada recursiva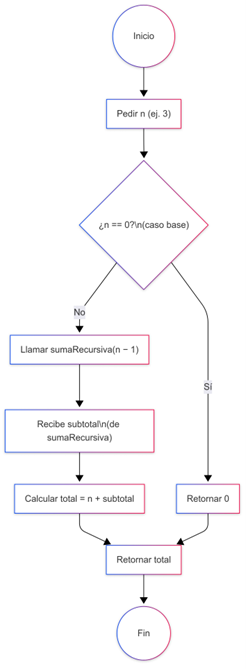

                        
                    

Figura 3: Diagrama de flujo para una función recursiva simple Fuente: Creación de autor, D. Nicolalde.

×

Descripción: Este diagrama ilustra cómo una función recursiva realiza llamadas a sí misma hasta que alcanza el caso base.

Calcular la suma de los primeros n números enteros:

                        
def suma_recursiva(n):
    if n == 1:  # Caso base
        return 1
    else:
        return n + suma_recursiva(n - 1)  # Llamada recursiva

resultado = suma_recursiva(5)
print(resultado)   # Imprime 15 (1+2+3+4+5)

                        
                    

• Caso base: Cuando n es 1, la función retorna 1 y termina.
• Llamada recursiva: Para valores mayores, la función suma n al resultado de la función llamada con n-1 hasta llegar al caso base.

El factorial de un número n, denotado como n!, es el producto de todos los números enteros desde 1 hasta n. Por ejemplo:

5! = 5 × 4 × 3 × 2 × 1 = 120

Un cálculo recursivo del factorial de n puede definirse de la siguiente manera:

• Caso base: El factorial de 0 es 1 (es decir, 0!=1).
• Llamada recursiva: El factorial de n es n×(n−1)!, por lo tanto, podemos hacer una llamada recursiva para calcular (n−1)!.

                        
def factorial(n):
    if n == 1:  # Caso base
        return 1
    else:
        return n * factorial(n - 1)  # Llamada recursiva

resultado = factorial(5)
print(resultado)  # Imprime 120 (5*4*3*2*1)

                        
                    

• La función factorial toma un número n y verifica si n es igual a 0. Si es así, retorna 1 (el caso base).
• Si n no es 0, entonces la función retorna el valor de n×(n−1)! y para calcular (n−1)!, la función se llama a sí misma con el valor de n−1. Este proceso se repite hasta que se llega al caso base.

Supongamos que queremos calcular 5!:

Esto hará lo siguiente:

1. factorial(5) retorna 5×factorial(4)
2. factorial(4) retorna 4×factorial(3)
3. factorial(3) retorna 3×factorial(2)
4. factorial(2) retorna 2×factorial(1)
5. factorial(1) retorna 1×factorial(0)
6. factorial(0) llega al caso base y retorna 1.

Ahora, todas las llamadas recursivas se resuelven:

• factorial(1) retorna 1×1=1
• factorial(2) retorna 2×1=2
• factorial(3) retorna 3×2=6
• factorial(4) retorna 4×6=24
• factorial(5) retorna 5×24=120

Finalmente, 5!=120

La recursión funciona porque se reduce el problema original a un problema más pequeño con cada llamada recursiva. Eventualmente, el problema alcanza el caso base, y a partir de allí las funciones se "desenrollan" y se resuelven paso a paso, volviendo al nivel original.

• Simplicidad: Los problemas complejos que pueden dividirse en subproblemas similares se resuelven de manera más sencilla con la recursión. En lugar de escribir un código largo y complicado, la recursión permite una solución más compacta y elegante.
• Legibilidad: El código recursivo es más fácil de entender y leer cuando el problema sigue una estructura recursiva (como los árboles, grafos o problemas matemáticos como el factorial).

• Uso de memoria: Las funciones recursivas pueden usar más memoria debido a la pila de llamadas (cada llamada recursiva consume memoria en la pila). Si el problema es demasiado grande o no tiene un caso base adecuado, puede llevar a un desbordamiento de pila.
• Rendimiento: En algunos casos, las funciones recursivas pueden ser más lentas que las iterativas debido al sobrecosto de las llamadas y retornos múltiples.

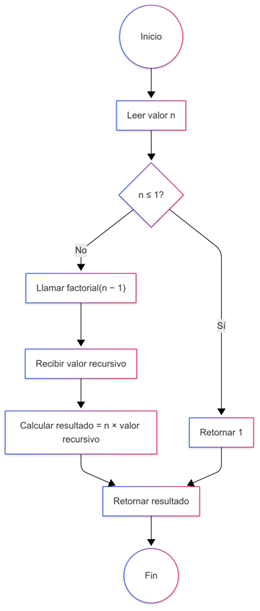
Figura 4: Diagrama de flujo para calcular el factorial de un número n de forma recursiva Fuente: Creación de autor, D. Nicolalde.

×

Descripción: Muestra cómo las llamadas recursivas permiten calcular el factorial de un número.

La secuencia de Fibonacci es una serie de números en la que cada número es la suma de los dos números anteriores. Comienza de la siguiente manera:

• Fibonacci(0) = 0
• Fibonacci(1) = 1
• Fibonacci(2) = Fibonacci(1) + Fibonacci(0) = 1 + 0 = 1
• Fibonacci(3) = Fibonacci(2) + Fibonacci(1) = 1 + 1 = 2
• Fibonacci(4) = Fibonacci(3) + Fibonacci(2) = 2 + 1 = 3
• Fibonacci(5) = Fibonacci(4) + Fibonacci(3) = 3 + 2 = 5
• Fibonacci(6) = Fibonacci(5) + Fibonacci(4) = 5 + 3 = 8

La secuencia de Fibonacci es fundamental en matemáticas y tiene aplicaciones en diversas áreas como la teoría de números, algoritmos de optimización, y la programación dinámica.

Una función recursiva es una función que se llama a sí misma para resolver un problema dividiéndolo en subproblemas más pequeños. La secuencia de Fibonacci es un ejemplo clásico donde cada número depende de los dos números anteriores. Para calcular, por ejemplo, Fibonacci(6), necesitamos saber Fibonacci(5) y Fibonacci(4), y para obtener estos, necesitamos calcular Fibonacci(4), Fibonacci(3), y así sucesivamente hasta llegar al caso base.

En una función recursiva, el caso base es esencial para detener las llamadas infinitas. En este caso, el caso base es cuando n es igual a 0 o 1, ya que los valores de Fibonacci(0) y Fibonacci(1) están definidos explícitamente como 0 y 1, respectivamente.

La secuencia de Fibonacci está definida como:

• Fibonacci(0) = 0
• Fibonacci(1) = 1
• Fibonacci(n) = Fibonacci(n-1) + Fibonacci(n-2) para n > 1.

                        
def fibonacci(n):
    if n <= 1:  # Caso base
        return n
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)  # Llamada recursiva

resultado = fibonacci(6)
print(resultado)  # Imprime 8 (la secuencia es 0, 1, 1, 2, 3, 5, 8)

                        
                    

1. Caso Base: En la función fibonacci(n), si n es igual o menor a 1 (es decir, 0 o 1), la función retorna n directamente.
   • Si n = 0, retorna 0.
   • Si n = 1, retorna 1.
   Este paso es crucial porque evita que la función se llame indefinidamente.
2. Llamada Recursiva: Si n es mayor que 1, la función no retorna un valor directamente. En lugar de eso, hace dos llamadas recursivas a la misma función:
   • fibonacci(n - 1)
   • fibonacci(n - 2)
   Luego, la función retorna la suma de estos dos resultados. Esto crea una estructura de llamadas que se van apilando hasta llegar a los casos base.
3. Resultado: Finalmente, cuando se calcula fibonacci(6):
   • La función primero llama a fibonacci(5) y fibonacci(4).
   • fibonacci(5) hace dos llamadas más a fibonacci(4) y fibonacci(3).
   • fibonacci(4) a su vez hace llamadas a fibonacci(3) y fibonacci(2), y así sucesivamente.
   Este proceso se sigue repitiendo hasta llegar a los casos base: fibonacci(1) y fibonacci(0).
4. La Estructura de Llamadas: Cuando se llama fibonacci(6), la secuencia de llamadas será algo así:

Este proceso va desglosando los números hasta llegar a los casos base, y luego suma los resultados cuando se "desenrollan" las llamadas recursivas.

Cuando llamamos a fibonacci(6), el resultado final será 8, ya que el número en la posición 6 de la secuencia de Fibonacci es 8.

Este ejemplo muestra cómo las funciones recursivas pueden ser útiles para resolver problemas en los que la solución depende de subproblemas más pequeños, como la secuencia de Fibonacci.

• Eficiencia: La recursión para la secuencia de Fibonacci no es eficiente para números grandes debido a las múltiples llamadas redundantes. Por ejemplo, fibonacci(6) hace fibonacci(5) y fibonacci(4), y ambos a su vez llaman a fibonacci(3), lo que resulta en una gran cantidad de cálculos repetidos.
• Optimización: Este tipo de recursión puede ser optimizado usando memorización o convirtiéndola en una solución iterativa para mejorar el rendimiento.

Usar memorización permite almacenar los resultados de las llamadas recursivas para que no se recalculen varias veces. Aquí tienes una versión optimizada de la función Fibonacci:

                        
def fibonacci_memorizado(n, memo={}):
    if n <= 1:  # Caso base
        return n
    if n not in memo:  # Si el valor no ha sido calculado antes
        memo[n] = fibonacci_memorizado(n - 1, memo) + fibonacci_memorizado(n - 2, memo)
    return memo[n]

                        
                    

• Usamos un diccionario memo para almacenar los resultados ya calculados.
• Si fibonacci(n) ya ha sido calculado, simplemente se retorna el valor guardado, evitando el cálculo redundante.

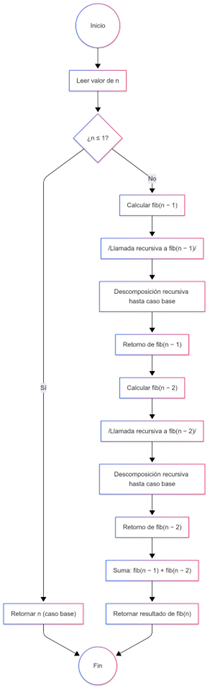
Figura 5: Diagrama de flujo para la secuencia de Fibonacci Fuente: Creación de autor, D. Nicolalde.

×

Descripción: Muestra cómo las llamadas recursivas se descomponen hasta llegar al caso base y luego se resuelven de vuelta.

Las funciones recursivas son una poderosa herramienta para resolver problemas que pueden descomponerse en subproblemas similares. Para que una función recursiva sea exitosa, debe contar con un caso base que detenga las llamadas infinitas y con una llamada recursiva que reduzca el problema a uno más simple. En el caso de la secuencia de Fibonacci, la recursión permite calcular cada número de manera eficiente, aunque puede ser optimizada para problemas más grandes.

La tabla 1 muestra los diferentes tipos de parámetros que se pueden utilizar en las funciones de Python. Incluye los parámetros posicionales, con valores predeterminados y los parámetros arbitrarios, lo que permite mayor flexibilidad al definir funciones.

En la tabla 2 se comparan las variables locales y globales, mostrando cómo se definen, cómo se acceden a ellas, y cómo se modifican dentro de las funciones.