-
Introducción
P
ython ha ganado gran popularidad debido a su facilidad de uso y su capacidad para escalar hacia aplicaciones más complejas. Desde simples scripts de automatización hasta sistemas de aprendizaje automático y aplicaciones web de gran escala, Python proporciona las herramientas necesarias para abordar una amplia gama de problemas. Su ecosistema, rico en bibliotecas como NumPy, Pandas, TensorFlow, Flask y Django, permite a los desarrolladores implementar soluciones avanzadas de manera eficiente. La comunidad activa de Python también asegura la constante mejora del lenguaje y sus herramientas, proporcionando soporte y recursos valiosos para el aprendizaje continuo y la resolución de problemas.
-
13. Programas más avanzados en Python13.1 Herramientas de cálculo con Python para modelaje de funciones aplicado a negocios: análisis marginal
A continuación, se presentan ejemplos de programas avanzados en Python en diversas áreas, ilustrando cómo este lenguaje puede utilizarse para resolver problemas complejos.
Ejemplo 1. Análisis de Datos con Pandas
Figura 57:
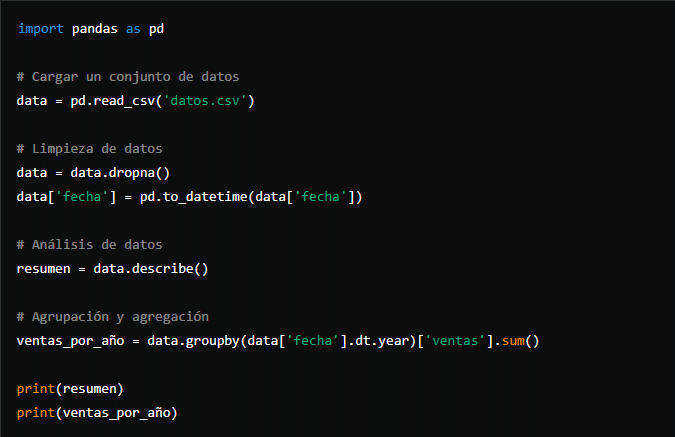
Este programa carga un conjunto de datos, realiza limpieza de datos, convierte una columna a formato de fecha, genera un resumen estadístico y agrupa las ventas por año. Ejemplo 2. Desarrollo Web con Flask
Figura 58
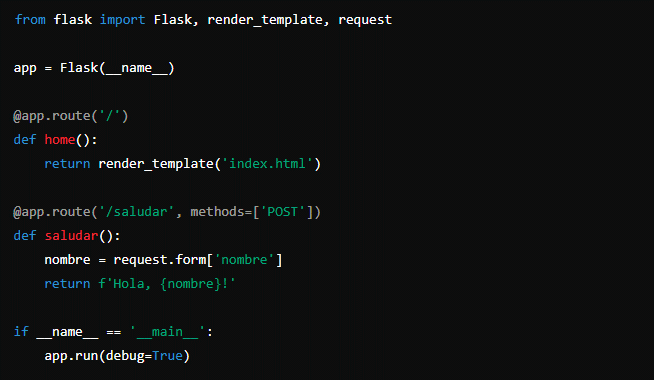
Este programa utiliza Flask para crear una aplicación web simple con una ruta de inicio y una ruta que procesa un formulario para saludar al usuario por su nombre. Ejemplo 3. Aprendizaje Automático con Scikit-Learn
Figura 59
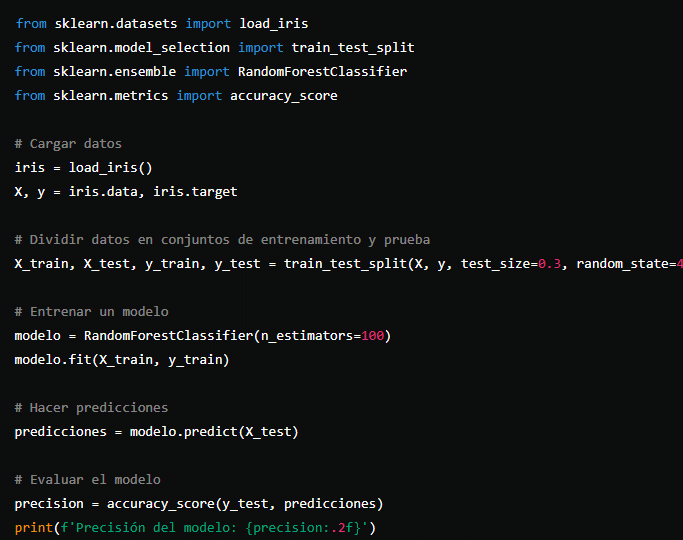
Este programa carga el conjunto de datos de iris, divide los datos en conjuntos de entrenamiento y prueba, entrena un modelo de bosque aleatorio y evalúa su precisión. 13.2 Herramientas de cálculo con Python para modelaje de funciones aplicado a negocios: oferta y demanda y producción totalEn esta sección, exploraremos cómo utilizar Python para analizar puntos críticos en funciones matemáticas aplicadas a los negocios. Nos centraremos en la identificación de máximos y mínimos relativos, así como en cómo estos conceptos se aplican en el análisis marginal de funciones de costo, ingreso y lucro. Estos conocimientos son esenciales para tomar decisiones estratégicas en un negocio.
Puntos críticos y máximos/mínimos relativos
Un punto crítico de una función se encuentra cuando su primera derivada respecto a x se iguala a cero. Matemáticamente, esto se expresa como: f′(x)=0.
El valor de x que satisface esta ecuación es el punto crítico. Este punto puede ser un máximo, un mínimo o un punto de inflexión.
Análisis de máximos y mínimos relativos
Criterio de la primera derivada: Para determinar si un punto crítico es un máximo o un , analizamos el signo de la primera derivada en intervalos cercanos a ese punto:
Si f′(x) es positiva en un intervalo y negativa en otro, el punto crítico es un .
Si f′(x) es negativa en un intervalo y positiva en otro, el punto crítico es un mínimo relativo.
Criterio de la segunda derivada: El criterio de la segunda derivada proporciona un método más directo para clasificar puntos críticos:
Si la segunda derivada f′′(x) evaluada en el punto crítico es menor que cero, el punto es un máximo relativo.
Si f′′(x) evaluada en el punto crítico es mayor que cero, el punto es un mínimo relativo.
Aplicación en negocios: análisis marginal
El análisis marginal se refiere a la evaluación de la tasa de cambio instantánea en funciones de negocio, tales como el costo, el ingreso y el lucro.
Funciones marginales
Costo marginal: El costo marginal se define como la derivada de la función de costo total C(x): C′(x). Representa la tasa instantánea de cambio del costo total con respecto al número de productos producidos.
Ingreso marginal: El ingreso marginal es la derivada de la función de ingreso total R(x): R′(x). Indica la tasa instantánea de cambio del ingreso total por cada unidad adicional vendida.
Lucro marginal: El lucro marginal es la derivada de la función de lucro total P(x), que es la diferencia entre ingreso y costo: P′(x)=R′(x)−C′(x)
Problema: Una compañía produce tanques de gasolina para autos. El costo total de producir x tanques está dado por la función C(x). Queremos encontrar el costo marginal y el costo exacto de producir un tanque adicional en un nivel de producción de 500 tanques por semana.
Solución: Definimos la función de costo total C(x) y calculamos su derivada.
Figura 60

Evaluamos el costo marginal en x=500:
Figura 61

Calculamos el costo exacto de producir el tanque 501:
Figura 62
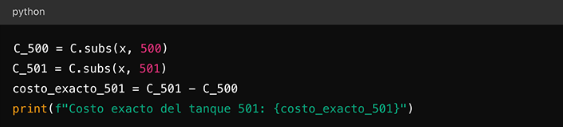
En esta sección, vamos a aplicar la teoría aprendida sobre costos, ingresos y lucros marginales utilizando Python. Esto nos permitirá visualizar de manera práctica cómo se comportan estas funciones en un entorno de negocios. ¡Vamos a preparar nuestro entorno y comenzar con los cálculos!
Preparación del entorno
Primero, necesitamos preparar nuestro entorno de trabajo en Python. Definiremos nuestras funciones de costo y precio para luego calcular el ingreso y el lucro.
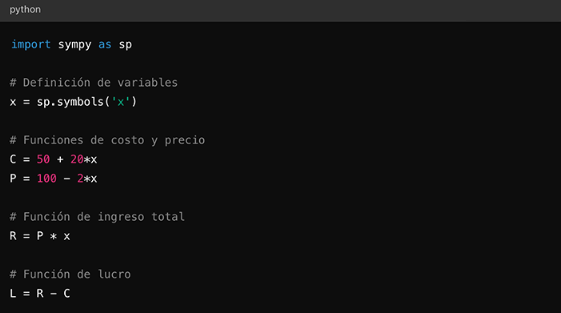
Definición de funciones
C(x)=50+20x
P(x)=100−2x
Figura 63
Derivadas y funciones marginales
C′(x)=d/dx(50+20x)
R′(x)=d/dx(P(x)⋅x)
L′(x)=d/dx(R(x)−C(x))
Figura 64

Visualización
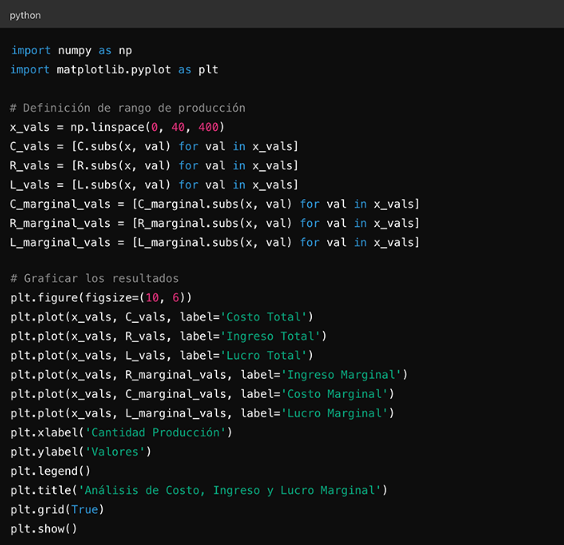
Para comprender mejor cómo se comportan estas funciones, vamos a visualizar los resultados en gráficos. Supongamos que estamos produciendo entre 0 y 40 unidades. Calcularemos y graficaremos el costo, el ingreso y el lucro total, así como sus derivadas marginales.
Figura 65
Interpretación de resultados Al visualizar los resultados, podemos observar lo siguiente:
- Costo total: Incrementa linealmente con la cantidad producida debido al término 20x.
- Ingreso total: Inicialmente incrementa, pero luego decrece debido a la función de demanda P(x).
- Lucro total: Es la diferencia entre el ingreso y el costo. Se observa el punto máximo de lucro.
- Ingreso marginal: Muestra cómo cambia el ingreso total con cada unidad adicional vendida.
- Costo marginal: Muestra cómo cambia el costo total con cada unidad adicional producida.
- Lucro marginal: Indica la rentabilidad de producir una unidad adicional.
Máximo relativo
Es el punto en una función donde el valor de la función es mayor que en los puntos inmediatamente adyacentes. También conocido como máximo local, es un punto x=c tal que f(c)≥f(x) para todos los x cercanos a c.
Mínimo relativo
Es el punto en una función donde el valor de la función es menor que en los puntos inmediatamente adyacentes. También conocido como mínimo local, es un punto x=c tal que f(c)≤f(x) para todos los x cercanos a c.