-
Introducción
Mostrar más Mostrar menosIntroducción
Queridos participantes,
¡Bienvenidos a esta emocionante aventura digital! Nos entusiasma ser parte de este viaje de aprendizaje, en el que descubrirán nuevas herramientas, adquirirán valiosos conocimientos y desarrollarán habilidades que les acompañarán a lo largo de su trayectoria.
Les invitamos a familiarizarse con la plataforma, conocer el curso y participar activamente.
¡Estamos aquí para apoyarlos en cada paso de este proceso!
¡Mucho éxito en este inicio!
El equipo de PUCE Virtual
-
Tutoriales
Sílabo
Manual del estudiante
-
Resultados de Aprendizaje y Criterios de Evaluación
La asignatura de Cálculo tiene como objetivo proporcionar una comprensión profunda de los conceptos fundamentales del cálculo diferencial e integral, así como su aplicación en diversas disciplinas. A lo largo de 16 semanas, los estudiantes desarrollarán un proyecto integral que les permitirá aplicar los conocimientos adquiridos en situaciones reales. Este enfoque práctico no solo reforzará su comprensión teórica, sino que también les brindará habilidades analíticas y de resolución de problemas esenciales para su futura carrera académica y profesional.
RESULTADOS DE APRENDIZAJE
RDA 1: Comprender los conceptos, definiciones, propiedades, reglas y teoremas fundamentales del cálculo diferencial e integral, de funciones reales de una variable en el campo de la Ingeniería
- Criterio de evaluación 1: Exactitud en la comprensión de los fundamentos de cálculo.
RDA 2: Calcular límites, derivadas e integrales de funciones de una variable con el apoyo de simuladores
- Criterio de evaluación 1: Eficacia en la resolución de problemas aplicados de cálculo.
RDA 3: Aplicar las herramientas del cálculo diferencial a la solución de problemas en diferentes contextos vinculados a la Ingeniería
- Criterio de evaluación 1: Aplica las herramientas de cálculo para optimización en un problema aplicado a negocios.
- Criterio de evaluación 2: Comprueba sus resultados con datos aplicados a modelos de negocios reales.
- Criterio de evaluación 3: Capacidad para implementar en código en Python el modelo de negocio usando cálculo.
-
Índice
Resultados de aprendizajeClases -
Mostrar más-
-
-
-
Introducción
Antes de adentrarse en los conceptos avanzados de cálculo, se repasarán algunos fundamentos esenciales, comenzando con las ecuaciones, es decir, qué son las ecuaciones, tanto las lineales como las de orden superior.
¿Qué es una ecuación?
Una ecuación es una igualdad entre dos expresiones, generalmente compuestas por coeficientes y letras que representan incógnitas. Por ejemplo, en la ecuación 3x−10=2x, el símbolo igual (=) indica la equivalencia entre las dos expresiones a ambos lados del signo.
-
1.1 Ecuaciones lineales
Una ecuación lineal, también conocida como ecuación de primer grado, es aquella que presenta una o más incógnitas elevadas a la potencia uno.
Estas ecuaciones son fundamentales en matemáticas debido a su simplicidad y amplia aplicación. Por ejemplo:
- 4x−20 = 12
- 5x−3 = 2x+8
En ambos casos, las incógnitas (x) están elevadas a la primera potencia, lo que las clasifica como ecuaciones lineales.
Resolución de ecuaciones lineales
Para resolver una ecuación lineal con una sola incógnita, se siguen estos pasos:
Aislar la incógnita:
- Mover los términos con incógnitas a un lado de la ecuación y los términos constantes al otro lado.
- Por ejemplo, para la ecuación 4x−20 = 12:
- Movemos el -20 al otro lado sumando 20 a ambos lados: 4x = 12+20
- Simplificamos: 4x = 32
Despejar la incógnita:
- Dividimos ambos lados por el coeficiente de x:
- x = 32/4
- Simplificamos: x = 8
Comprobación
Para comprobar la solución, sustituimos x = 8 en la ecuación original: 4(8) – 20 = 32 – 20 = 12 La igualdad se cumple, confirmando que x = 8 es la solución correcta. -
1.2 Funciones racionales y polinómicasLas funciones racionales y polinómicas son fundamentales en el estudio del cálculo y tienen amplias aplicaciones en diversas áreas de las matemáticas y las ciencias aplicadas. A continuación, se presentan sus características, propiedades y ejemplos.
1.2.1. Funciones polinómicas
Las propiedades más importantes de las funciones polinómicas incluyen:Donde an,…,a0 son coeficientes reales y n es el grado del polinomio.
- Continuidad y derivabilidad: Las funciones polinómicas son continuas y derivables en todos los puntos de su dominio, que es todo el conjunto de números reales (Blanco & García, 2019).
- Crecimiento y comportamiento asintótico: El comportamiento de una función polinómica a medida que x tiende a infinito está determinado por su término de mayor grado.
Ejemplo:
1.2.2. Funciones racionales
Las funciones racionales se definen como el cociente de dos funciones polinómicas.Las propiedades de las funciones racionales incluyen:Donde Q(x)≠0 y P,Q son polinomios.
- Dominio: El dominio de una función racional es el conjunto de todos los números reales, excepto aquellos que hacen que Q(x)=0 (López & Torres, 2020).
- Asíntotas: Las funciones racionales pueden tener asíntotas verticales (cuando Q(x)=0 y horizontales (determinadas por el grado de los polinomios en el numerador y el denominador).
Ejemplo:
Las funciones racionales y polinómicas son esenciales en el análisis matemático y tienen aplicaciones en la modelización de fenómenos naturales, optimización y otras áreas de la ciencia y la ingeniería (Martínez & Pérez, 2018). -
1.3 Funciones aplicadas a modelo de negocios: costo, precio unitario, ingreso y lucro
Las funciones matemáticas son herramientas fundamentales para analizar y comprender los modelos de negocio. A continuación, se presentan algunas de las funciones clave relacionadas con el costo, el precio unitario, el ingreso y el lucro, y cómo se aplican en el contexto empresarial.
1.3.1. Función de costo (C)
La función de costo se refiere a la relación entre el costo total de producción y la cantidad producida. Se puede expresar como:
Donde representa los costos fijos (independientes de la cantidad producida) y los costos variables (dependientes de la cantidad producida ).
Esta función es esencial para determinar el nivel de producción óptimo y la estructura de costos de una empresa (Gómez & Rodríguez, 2019).
1.3.2. Función de precio unitario (P)
El precio unitario es el costo que un cliente debe pagar por cada unidad de producto. Este puede ser constante o variar según la cantidad producida o vendida. Matemáticamente, se puede representar como:
El precio unitario es crucial para establecer estrategias de precios y maximizar la competitividad en el mercado (Martínez & López, 2020).
1.3.3. Función de ingreso (R)
El ingreso total (R) es el resultado de multiplicar la cantidad vendida (q) por el precio unitario (P). Se representa como:
Esta función ayuda a las empresas a comprender cómo varía el ingreso con cambios en la cantidad de producto vendido y el precio unitario, permitiendo la planificación de ingresos y estrategias de ventas (Pérez & Sánchez, 2018).
1.3.4. Función de lucro (L)
El lucro o beneficio es la diferencia entre el ingreso total (R) y el costo total (C). Matemáticamente, se expresa como:
L(q)=R(q)-C(q)
Esta función es fundamental para evaluar la rentabilidad de un negocio. Un análisis detallado de la función de lucro permite a las empresas tomar decisiones informadas sobre producción, precios y estrategias de mercado (Torres & Castillo, 2021).
-
1.4 Límites y asíntotas verticales y horizontales
En este tema se aborda la definición de límite, sus aplicaciones en diversos campos, como la ingeniería, y algunos ejemplos prácticos con funciones racionales y polinómicas
1.4.1. ¿Qué es un límite?
El límite es un concepto fundamental en cálculo y análisis matemático. Sirve como base para definir ideas cruciales como la continuidad, las derivadas y las integrales. El límite de una función en un punto describe el comportamiento de esa función cuando sus entradas se aproximan a un valor específico, aunque nunca alcancen ese valor exacto.
Aplicaciones prácticas de los límites
Los límites tienen múltiples aplicaciones prácticas en campos como:
- Ingeniería: Permiten calcular la eficiencia máxima de una máquina en condiciones ideales.
- Física: Ayudan a modelar fenómenos naturales y comportamientos físicos.
- Economía: Se utilizan para modelar el crecimiento o decrecimiento hacia un punto de estabilidad.
Definición matemática de límite
Matemáticamente, el límite de una función se expresa como sigue:Esto significa que el valor de se puede hacer tan cercano como se desee a un número , siempre que esté suficientemente cerca de , pero no necesariamente igual a .
Ejemplos de límites
A continuación, se presentan algunos ejemplos para entender mejor cómo funcionan los límites.
Ejemplo 1: Función Lineal
Calculemos el límite de la función 3x+1 cuando x tiende a 2:
Simplemente reemplazamos x por 2 en la función:
3(2)+1=6+1=7
Por lo tanto, el límite es 7.
Ejemplo 2: Función con infinito
Calculemos el límite de la función 1x−5 cuando x tiende a infinito:
Si x es un número muy grande, x−5 sigue siendo muy grande, y la fracción se aproxima a cero:
Por lo tanto, el límite es 0.
Ejemplo 3: Función racional
Calculemos el límite de la función x2−9x−3 cuando x tiende a 3:
Primero, sustituimos x por 3, lo que nos da una indeterminación 0/0. Para resolverlo, factorizamos el numerador:
Sustituyendo en la función original, obtenemos:
Simplificamos:
Ahora, calculamos el límite:
Por lo tanto, el límite es 6.
Los límites son una herramienta esencial en cálculo y tienen aplicaciones prácticas en múltiples disciplinas. En la próxima clase, se continuará explorando más ejemplos y problemas para afianzar estos conceptos.
-
Profundiza más
Este video te ayudará a enfatizar sobre Ecuaciones Lineales ¡Accede aquí!
Aprende más
Para enriquecer sus conocimientos, revisa lo siguiente “Documento - Análisis de Funciones Exponenciales, Racionales y Logarítmicas ¡Accede aquí!
Profundiza más
Este video te ayudará a enfatizar sobre Limites ¡Accede aquí!
Aprende más
Para enriquecer sus conocimientos, revisa lo siguiente “Tutorial sobre Asíntotas Verticales y Horizontales”. ¡Accede aquí!
-
-
-
Introducción
E
l cálculo en una dimensión, también conocido como cálculo diferencial e integral de funciones de una variable, es una rama fundamental de las matemáticas que se enfoca en el estudio de las tasas de cambio y la acumulación de cantidades. A continuación, se presentan los conceptos clave y las aplicaciones principales de este campo. Los límites son la base del cálculo diferencial.
Un límite describe el valor al que una función se aproxima a medida que la variable independiente se acerca a un cierto punto. La continuidad de una función en un punto significa que el límite de la función en ese punto es igual al valor de la función en ese punto (García & Rodríguez, 2019).
Ejemplo:
Fórmula
En este caso, f(x) se aproxima a L cuando x se aproxima a c.
-
2.1 Derivada: concepto y derivadas de funciones racionales, polinómicas y exponenciales2.2. Derivadas y puntos críticos
En esta sección, se ingresará al fascinante mundo de las derivadas y su conexión con los límites. Se analizarán sus características principales, se revisarán tablas de fórmulas y se aprenderá cómo aplicarlas en situaciones del mundo real.
Las derivadas son una herramienta fundamental en el cálculo diferencial. Permiten estudiar cómo cambian las funciones cuando sus variables de entrada también cambian. La derivada de una función en un punto específico puede interpretarse como la pendiente de la línea tangente a la gráfica de la función en ese punto. La derivada de una función mide la tasa de cambio instantánea de la función con respecto a una variable. Se define como el límite del cociente incremental cuando el incremento tiende a cero:
Fórmula
Las derivadas tienen múltiples aplicaciones, incluyendo la determinación de máximos y mínimos de funciones, el estudio del comportamiento de funciones y la resolución de problemas de optimización (Pérez & Torres, 2020).
Por ejemplo, si se tiene una función f(x), la derivada en un punto dado nos ayuda a encontrar la pendiente de la recta tangente en ese punto. Esta pendiente es crucial en diversos campos, como la física.
Matemáticamente, la derivada es el límite de la razón de cambio promedio en un intervalo cada vez más pequeño.
La derivada de una función f(x) en el punto x=a se define como:
Fórmula
En esta definición, h representa un incremento muy pequeño en la variable x. Imagine medir la velocidad de un automóvil: si se quiere saber su velocidad exacta en un instante específico, se necesita un intervalo de tiempo extremadamente pequeño.
A medida que ese intervalo h tiende a cero, la razón de cambio promedio se convierte en la derivada.
Ejemplo práctico: Derivada de x^2Tomemos la función f(x)= x^2 y calculemos su derivada usando la definición:
Fórmula
Se desarrolla la expresión en el numerador:
Fórmula
Luego, se simplifica:
Fórmula
Por lo tanto, la derivada de x^2 es 2x. Este proceso puede parecer largo, pero nos proporciona una comprensión profunda de cómo funcionan las derivadas.
Aunque se puede calcular derivadas utilizando la definición de límite, este proceso puede ser tedioso para funciones más complejas. Por eso, se utilizan tablas de derivadas que resumen los resultados de estas operaciones. En la siguiente parte del curso, se revisará cómo usar estas tablas para simplificar el cálculo de derivadas de diversas funciones.
2.3. Herramientas tecnológicas para el cálculo de derivadasEn esta sección, se aborda uno de los conceptos centrales en el estudio de las derivadas: las derivadas y los puntos críticos.
Para comenzar, se explica cómo se calcula la derivada de una función polinómica utilizando la fórmula básica f(x)=ax^n.
Fórmula
donde a y n son números reales.
Ejemplo de derivada polinómica
Considera la función f(x)=3x4+1. Se quiere hallar su derivada.
Las constantes que multiplican a x simplemente se mantienen, y se aplica la fórmula a la derivada de x^4:
Fórmula
Por lo tanto, la derivada de
Fórmula
es
Fórmula
Derivada de funciones racionales
Ahora, considera la función
Fórmula
una función racional, ya que es el cociente entre dos funciones polinómicas. Se utiliza la fórmula para la derivada de un cociente de funciones:
Fórmula
En este caso
Fórmula
/p>
Se calculan las derivadas:
Fórmula
Se aplican estas derivadas a la fórmula del cociente:
Fórmula
Se simplifican los términos:
Fórmula
Por lo tanto, la derivada de
Fórmula
es
Fórmula
2.4. Regla de la cadenaPara facilitar el cálculo de derivadas, podemos utilizar herramientas como Wolfram Alpha. Esta plataforma permite calcular derivadas, integrales y más utilizando entradas matemáticas.
La versión gratuita proporciona resultados, aunque para ver los pasos detallados es necesario optar por la versión de pago. Esta herramienta puede ser de gran ayuda en la resolución de problemas relacionados con derivadas.
Los puntos críticos de una función son aquellos en los que la derivada es cero o no existe. Para encontrarlos, utilizamos el criterio de la primera derivada. Derivamos la función y luego igualamos la derivada a cero. Los valores de x que satisfacen esta ecuación son los puntos críticos.
Considera la función
Fórmula
Se deriva la función:
Fórmula
Se iguala la derivada a cero para encontrar los puntos críticos:
Fórmula
Por lo tanto, x=-1 es un punto crítico de la función
Fórmula
2.5. Tasa de CambioEn cálculo, la regla de la cadena y el concepto de tasa de cambio son fundamentales para comprender cómo varían las funciones compuestas y cómo se miden los cambios en una variable con respecto a otra. La regla de la cadena es una fórmula utilizada para calcular la derivada de una función compuesta.
Si se tiene dos funciones, f(u) y g(x), donde u=g(x), entonces la derivada de la función compuesta f(g(x)) con respecto a x se calcula como:
Fórmula
Es decir, la derivada de la función externa f evaluada en la función interna g(x), multiplicada por la derivada de la función interna g(x). Este método es esencial para el cálculo de derivadas en funciones donde una variable depende de otra (López & Pérez, 2019).
Ejemplo:
Si
Fórmula
entonces la derivada
Fórmula
se calcula usando la regla de la cadena.
La tasa de cambio de una función describe cómo una cantidad varía en relación con otra. Matemáticamente, se expresa como la derivada de la función. En el contexto de una función y=f(x), la tasa de cambio de y con respecto a x se da por:
Fórmula
La tasa de cambio puede interpretarse como la pendiente de la recta tangente a la curva de la función en un punto dado. Es útil en numerosos campos para describir fenómenos como velocidad, aceleración, crecimiento económico, entre otros (Gómez & Sánchez, 2020).
2.6. Máximos y mínimos: criterio de la primera y segunda derivada
En cálculo, identificar los puntos donde una función alcanza máximos y mínimos es fundamental para el análisis de funciones. Estos puntos pueden ser máximos o mínimos locales o globales y se determinan utilizando los criterios de la primera y segunda derivada.
El criterio de la primera derivada se utiliza para identificar los puntos críticos de una función, donde la pendiente de la tangente es cero o no existe. Un punto crítico ocurre cuando f′(x)=0 o f′(x) no está definida. Para determinar si estos puntos son máximos, mínimos o puntos de inflexión, se sigue el siguiente procedimiento:
- Encontrar la derivada de la función f′(x)
- Solucionar f′(x)=0 para encontrar los puntos críticos.
- Determinar el signo de f′(x) a la izquierda y derecha de cada punto crítico:
- Si f′(x) cambia de positivo a negativo, el punto crítico es un máximo local.
- Si f′(x) cambia de negativo a positivo, el punto crítico es un mínimo local.
El criterio de la primera derivada ayuda a analizar el comportamiento de una función y a encontrar los intervalos de aumento y disminución (Martínez & López, 2019).
El criterio de la segunda derivada se utiliza para determinar la concavidad de la función y confirmar si los puntos críticos son máximos o mínimos locales. Se basa en el análisis de la segunda derivada, f′(x):
- Calcular la segunda derivada f′′(x)
- Evaluar f′′(x) en los puntos críticos encontrados:
- Si f′′(x)>0 en un punto crítico, la función tiene un mínimo local en ese punto.
- Si f′′(x)<0 en un punto crítico, la función tiene un máximo local en ese punto.
- Si f′′(x)=0, el criterio es inconcluso, y se necesita más análisis.
Este criterio es útil para confirmar los resultados obtenidos con el criterio de la primera derivada y para entender la curvatura de la función (Gómez & Rodríguez, 2020).
Ejemplo
Para la función
Fórmula
aplicamos estos criterios para identificar y clasificar los puntos críticos.
-
Profundiza más
Este video te ayudará a enfatizar sobre Derivadas Parte 1 ¡Accede aquí!
Aprende más
Para enriquecer sus conocimientos, revisa lo siguiente “Tutorial sobre la Regla de L’Hôpital y Razones de Cambio” ¡Accede aquí!
Profundiza más
Este video te ayudará a enfatizar sobre Derivadas Parte 2 ¡Accede aquí!
Aprende más
Para enriquecer sus conocimientos, revisa lo siguiente “Tutorial sobre Análisis Gráfico con Derivadas”. ¡Accede aquí!
-
-
-
Introducción
E
l estudio de las gráficas de funciones mediante herramientas del cálculo es fundamental para comprender el comportamiento y las propiedades de las funciones matemáticas. Este análisis incluye el uso de derivadas para identificar características clave como máximos, mínimos, puntos de inflexión y asíntotas, así como para entender el crecimiento y decrecimiento de las funciones.
-
3.1 Gráficas con Cálculo3.2 Cálculo integral
3.1.1 Análisis de derivadas
Las derivadas juegan un papel crucial en el análisis de gráficas de funciones:
- Primera derivada y crecimiento/decrecimiento: La primera derivada de una función, f^' (x), indica la pendiente de la tangente a la curva en un punto dado.
- Segunda derivada y concavidad: La segunda derivada, f^'' (x), proporciona información sobre la concavidad de la función. Si f^'' (x)>0, la función es cóncava hacia arriba en ese intervalo, lo que indica que la pendiente está aumentando. Si f^'' (x)<0, la función es cóncava hacia abajo, indicando una pendiente decreciente.
- Puntos críticos y puntos de inflexión: Los puntos críticos ocurren donde la primera derivada es cero o no está definida, lo que indica posibles máximos, mínimos o puntos de inflexión. Un punto de inflexión es donde la concavidad de la función cambia, identificable por el cambio de signo en la segunda derivada (Gómez & López, 2019).
Si f^' (x)>0 en un intervalo, la función está creciendo en ese intervalo; si f^' (x)<0, la función está decreciendo.
3.1.2 Asíntotas
El cálculo también permite identificar asíntotas, que son líneas a las que la gráfica de la función se aproxima, pero nunca toca.
- Asíntotas verticales: Ocurren cuando el denominador de una función racional se acerca a cero, lo que hace que la función tienda a infinito.
- Asíntotas horizontales: Se encuentran observando el comportamiento de la función cuando x tiende a infinito positivo o negativo. Son particularmente útiles para funciones racionales.
Las integrales definidas se utilizan para calcular el área bajo una curva, lo cual es una aplicación crucial en muchos campos, incluida la economía y la física. La integral de una función en un intervalo específico también puede interpretarse como el acumulado neto de la función en ese intervalo.
3.1.3 Trazado de gráficas con herramientas computacionales
El uso de herramientas computacionales como Python (con bibliotecas como Matplotlib y Seaborn) facilita el trazado y análisis de gráficas de funciones.
Estas herramientas permiten:
- Visualización precisa: Trazado de curvas y líneas tangentes, identificación de puntos críticos y áreas bajo la curva.
- Análisis numérico: Aproximación de derivadas e integrales para funciones complejas que no tienen solución analítica simple.
- Interactividad: Modificación de parámetros en tiempo real para observar cómo cambian las características de la gráfica (Martínez & Torres, 2020).
Ejemplo Práctico
Para una función
Fórmula
el análisis de sus derivadas puede ayudar a identificar máximos y mínimos locales, así como puntos de inflexión.
La primera derivada,
Fórmula
y la segunda derivada,
Fórmula
se usan para este análisis.
3.1.4 Máximos y mínimos de funciones y aplicaciones a funciones en negocios
Los conceptos de máximos y mínimos de funciones son fundamentales en el cálculo y tienen aplicaciones cruciales en diversos campos, incluidos los negocios. Estas técnicas permiten identificar puntos de interés en funciones que modelan fenómenos económicos y empresariales, como costos, ingresos y beneficios.
Los máximos y mínimos de una función se refieren a los puntos donde la función alcanza sus valores más altos o más bajos, respectivamente. Estos puntos pueden ser locales (relativos a un intervalo específico) o globales (en todo el dominio de la función). Para identificar estos puntos, se utilizan principalmente dos criterios:
- Criterio de la primera derivada: Consiste en encontrar los puntos críticos donde la derivada de la función se anula o no existe. Luego, se analiza el signo de la derivada alrededor de estos puntos para determinar si son máximos o mínimos locales.
- Criterio de la segunda derivada: Se usa para confirmar la naturaleza de los puntos críticos, verificando la concavidad de la función en esos puntos. Si la segunda derivada es positiva, el punto crítico es un mínimo local; si es negativa, es un máximo local (Gómez & Pérez, 2019).
En el contexto de los negocios, encontrar los máximos y mínimos de funciones es esencial para la toma de decisiones estratégicas. Algunas aplicaciones clave incluyen:
- Optimización de costos: Determinar el nivel de producción que minimiza los costos totales. Por ejemplo, si C(q) es la función de costo en términos de la cantidad producida q, encontrar q que minimiza C(q) es crucial para la eficiencia operativa.
- Maximización de ingresos: Identificar el precio de venta óptimo o la cantidad de producto que maximiza los ingresos. Si R(q) = p(q)⋅q es la función de ingreso, donde p(q) es el precio como función de la cantidad, el objetivo es maximizar R(q) (López & Martínez, 2020).
- Maximización de beneficios: Las empresas buscan maximizar sus beneficios, definidos como la diferencia entre ingresos y costos. La función de beneficio B(q)=R(q)−C(q) puede ser analizada para encontrar el nivel de producción q que maximiza el beneficio.
Estas aplicaciones permiten a las empresas tomar decisiones informadas sobre producción, precios y estrategias de mercado, optimizando así su desempeño financiero y competitivo (Rodríguez & Torres, 2018).
Ejemplo
Una empresa que produce un bien tiene la función de costo y la función de ingreso . Para maximizar el beneficio, se derivan estas funciones y se aplican los criterios mencionados.
3.1.5 Asíntotas verticales y horizontales: costo promedio
En el análisis de funciones, las asíntotas verticales y horizontales son herramientas clave para entender el comportamiento de las funciones racionales y otros tipos de funciones. Estos conceptos también se aplican en el análisis de costos en contextos empresariales, especialmente en el cálculo del costo promedio.
Una asíntota vertical se presenta en una función
f ( x ) cuando la función tiende a infinito positivo o negativo a medida que la variable independientex se aproxima a un valor específico desde la izquierda o la derecha.Formalmente, si o , entonces
x = c es una asíntota vertical. Las asíntotas verticales suelen ocurrir en funciones racionales, donde el denominador se anula. Por ejemplo, para la función , existe una asíntota vertical en
x = 2 (López & Torres, 2019).Las asíntotas horizontales describen el comportamiento de una función a medida que la variable independiente tiende a infinito positivo o negativo.
Si o , donde
L es un número finito, entoncesy = L es una asíntota horizontal.Estas asíntotas son comunes en funciones donde el grado del numerador es menor o igual al grado del denominador. Por ejemplo, para la función , la asíntota horizontal es
y = 0 (Martínez & Gómez, 2020).El concepto de costo promedio se utiliza en economía y gestión de negocios para entender cómo varía el costo de producción por unidad a medida que se produce una mayor cantidad de bienes.
Se define como: donde
C ( q ) es el costo total de producirq unidades yC _ avg ( q ) es el costo promedio por unidad. El análisis deC _ avg ( q ) puede revelar la presencia de economías de escala, donde el costo promedio disminuye a medida que aumenta la producción (Pérez & Rodríguez, 2021).Las asíntotas horizontales y verticales en el gráfico de la función de costo promedio pueden proporcionar información sobre los costos fijos y variables a largo plazo. Por ejemplo, una asíntota horizontal en el costo promedio sugiere un costo constante por unidad a medida que la producción se incrementa indefinidamente, lo cual es típico en industrias con costos variables bajos.
3.2.1 Integral indefinida y ejemplos
En esta clase, se introducirá el concepto de la integral indefinida. La definición formal de una integral indefinida nos dice que es el conjunto de todas las funciones
F ( x ) cuyas derivadas sonf ( x ) . Es decir, la derivada deF ( x ) debe ser igual af ( x ): Fórmula
Por lo tanto,
f ( x ) se denomina primitiva de la funciónf ( x ) .La Integral como operación inversa
Se puede entender la integral indefinida como una operación inversa a la derivada. Mientras que en la derivada partimos de una función F(x) y obtenemos otra función f(x), en la integral indefinida hacemos lo contrario: partimos de f(x) y queremos encontrar F(x), su primitiva.
Para visualizar esto, imaginen que tienen una máquina (función F(x)) y solo conocen las piezas que la componen (función f(x)). Al juntar todas las piezas de manera correcta, obtenemos la máquina original. Aquí, las piezas representan la función f(x) y la máquina completa es f(x).
Una de las fórmulas fundamentales para la integral indefinida es:
Fórmula
donde C es la constante de integración. Es importante que n sea diferente de -1 para evitar una indeterminación.
Ejemplo de Integración
Consideremos la función polinómica
Si se quiere hallar su integral indefinida, se procede de la siguiente manera:
Se aplica la fórmula de la integral a cada término:
Se combina estos resultados para obtener la integral completa:
Las integrales son fundamentales en diversas áreas, como los negocios, la economía y la ingeniería. Por ejemplo, en el análisis de costos, ingresos y beneficios, las funciones polinómicas se utilizan comúnmente para modelar diversas situaciones.
3.2.2 Integral definida: cálculo de áreas
En esta sección, abordaremos la integral definida como la última parte de nuestro primer reto. La integral definida nos permite calcular el área bajo una curva, representada por la función f(x), entre dos límites, a y b.
La integral definida se utiliza para encontrar el área bajo una curva f(x) entre los puntos a y b. Este concepto fue desarrollado por el matemático Riemann, quien propuso una técnica que utiliza rectángulos para aproximar el área bajo la curva.
3.2.2.1. Método de Riemann
Riemann sugirió que el área bajo la curva se puede aproximar sumando las áreas de múltiples rectángulos formados bajo la curva. Al aumentar el número de rectángulos, la aproximación se vuelve más precisa. La clave es que estos rectángulos tienen una base Δx y una altura f(x).
Base del rectángulo: Δx
Altura del rectángulo: f(x)
El área de cada rectángulo es Δx⋅f(x). Sumando las áreas de todos los rectángulos, obtenemos una aproximación del área total bajo la curva.
Hacia la integral definida
Mientras más rectángulos usemos, más pequeños serán los intervalos Δx, acercándose a cero. En ese punto, la sumatoria de áreas se convierte en una integral:
Esto representa el área exacta bajo la curva f(x) entre los límites a y b.
Ejemplo práctico
Para ilustrar este concepto, consideremos la función f(x)=x2 y calculemos el área bajo esta curva desde x=0 hasta x=3:
Resolución paso a paso
Encontrar la primitiva de f(x): La primitiva de x^2 es x^3/3.
Evaluar la primitiva en los límites: Se evalúa la primitiva en el límite superior y luego en el límite inferior:
Simplificar la evaluación:
Por lo tanto, el área bajo la curva x2 desde x = 0 hasta x = 3 es 9 unidades cuadradas.
La integral definida es una herramienta poderosa en cálculo que nos permite determinar áreas bajo curvas con precisión. En futuras sesiones, exploraremos más ejemplos y problemas que solidifiquen este concepto.
-
Profundiza más
Este video te ayudará a enfatizar sobre Integrales Parte 1 ¡Accede aquí!
Aprende más
Para enriquecer sus conocimientos, revisa lo siguiente “Técnica de Integración por Cambio de Variable o Sustitución”. ¡Accede aquí!
Profundiza más
Este video te ayudará a enfatizar sobre Integrales Parte 2 ¡Accede aquí!
Aprende más
Para enriquecer sus conocimientos, revisa lo siguiente Técnica de Integración por Partes”. ¡Accede aquí!
-
-
-
-
Cálculo aplicado a situaciones reales de ingeniería y negocios y aplicaciones de integral definida
-
Introducción
E
l cálculo, tanto diferencial como integral, es una herramienta fundamental en la resolución de problemas en ingeniería y negocios. Su capacidad para modelar y analizar situaciones cambiantes permite a los profesionales en estas áreas optimizar procesos, predecir comportamientos y tomar decisiones informadas.
-
4.1. Cálculo aplicado a situaciones reales de ingeniería y negocios4.2 Aplicaciones de integral definida
En ingeniería, el cálculo se utiliza en diversas disciplinas para modelar fenómenos físicos, optimizar sistemas y diseñar estructuras. Algunas aplicaciones incluyen:
- Dinámica de fluidos: El cálculo diferencial es crucial para describir el flujo de fluidos mediante ecuaciones diferenciales parciales, como las ecuaciones de Navier-Stokes, que modelan la velocidad y presión de los fluidos en movimiento (González & Martínez, 2019).
- Electromagnetismo: Las leyes de Maxwell, fundamentales para el electromagnetismo, se expresan en términos de cálculo diferencial e integral, describiendo cómo los campos eléctricos y magnéticos interactúan y se propagan (Pérez & López, 2020).
- Análisis estructural: En ingeniería civil y mecánica, el cálculo se usa para determinar el comportamiento de estructuras bajo carga, incluyendo el cálculo de tensiones y deformaciones para asegurar la estabilidad y seguridad de los diseños.
El cálculo también es indispensable en el análisis y toma de decisiones en el ámbito empresarial. Sus aplicaciones en negocios incluyen:
- Optimización de costos y beneficios: Las empresas utilizan el cálculo para encontrar el nivel de producción o precio que maximiza los beneficios o minimiza los costos. Esto se logra identificando puntos críticos de funciones de costo y beneficio mediante derivadas (López & Torres, 2018).
- Análisis de crecimiento y decadencia: Las funciones exponenciales y logarítmicas, y sus derivadas, permiten modelar y analizar el crecimiento de ventas, población o inversiones, así como la depreciación de activos.
- Gestión de inventarios: El cálculo integral se aplica para prever la demanda y optimizar el nivel de inventarios, minimizando costos de almacenamiento y evitando el desabastecimiento (Rodríguez & Sánchez, 2021).
Ejemplo Práctico: Optimización de la producción
Un ejemplo de aplicación del cálculo en negocios es la optimización de la producción. Supongamos que una empresa tiene la función de costo total , donde es la cantidad de productos fabricados. La derivada de esta función, , se utiliza para encontrar el nivel de producción que minimiza los costos.
4.1.1 Costo y lucro marginal
El concepto de costo y lucro marginal es fundamental en el análisis económico y empresarial. Estos conceptos permiten a las empresas evaluar el impacto de producir y vender unidades adicionales de un bien o servicio, proporcionando una guía para la toma de decisiones estratégicas.
El costo marginal es el incremento en el costo total que resulta de producir una unidad adicional de un bien.
Matemáticamente, se define como la derivada del costo total con respecto a la cantidad producida, es decir:
donde C(q) es la función de costo total y q es la cantidad de unidades producidas. El costo marginal es crucial para las decisiones de producción, ya que ayuda a determinar si es rentable producir más unidades (Gómez & López, 2019).
Ejemplo:
Si una empresa tiene una función de costo total:
El costo marginal se calcula como:
Esto indica cómo cambia el costo total al producir una unidad más.
El lucro marginal es el cambio en el beneficio total que se obtiene al vender una unidad adicional de un producto. Se calcula como la diferencia entre el ingreso marginal y el costo marginal.
Matemáticamente, se define como:
Donde L(q) es la función de lucro, R(q) es la función de ingreso total, y C(q) es la función de costo total.
El lucro marginal es una herramienta clave para las empresas en la determinación del nivel de producción que maximiza las ganancias (Martínez & Torres, 2020).
El análisis de costos y lucros marginales es esencial para:
- Decisiones de producción: Las empresas deben producir hasta el punto donde el ingreso marginal sea igual al costo marginal para maximizar el beneficio.
- Determinación de precios: Al entender el costo marginal, las empresas pueden establecer precios que cubran estos costos y maximicen el beneficio.
- Eficiencia operacional: El análisis marginal ayuda a identificar ineficiencias y áreas donde los costos pueden ser reducidos sin afectar negativamente la producción.
La integral definida es una herramienta poderosa en el cálculo, utilizada para calcular el área bajo una curva, entre otros usos. Sus aplicaciones abarcan diversas disciplinas, incluyendo física, ingeniería, economía y más.
A continuación, se describen algunas de las aplicaciones más comunes y prácticas de la integral definida.
Cálculo de áreas
Una de las aplicaciones más directas de la integral definida es el cálculo del área bajo una curva sobre un intervalo [a,b]. Si f(x) es una función continua en este intervalo, el área bajo la curva desde a hasta b se calcula como:
Este concepto es fundamental para determinar áreas en geometría y para resolver problemas de distribución de probabilidad en estadística (González & Martínez, 2019).
La integral definida también se utiliza para calcular volúmenes de sólidos generados al rotar una curva alrededor de un eje.
Dos métodos principales para calcular el volumen de un sólido de revolución son:
- Método de los Discos: Se usa cuando se rota alrededor de un eje horizontal o vertical. El volumen se calcula como:
- Método de las Cáscaras CilíndricasEste método es aplicable cuando se rota alrededor de un eje que no está en contacto directo con la función. El volumen se calcula como:
Estas técnicas son esenciales en ingeniería y diseño industrial para calcular volúmenes de objetos complejos (Pérez & López, 2020).
En física, la integral definida se utiliza para calcular el trabajo realizado por una fuerza variable a lo largo de una distancia. Si una fuerza F(x) actúa sobre un objeto desplazado a lo largo del eje x desde a hasta b, el trabajo realizado es:
Este cálculo es fundamental en mecánica para determinar la energía requerida o generada en procesos físicos (Rodríguez & Torres, 2021).
En economía, la integral definida se utiliza para encontrar el valor presente de flujos de ingresos o gastos continuos. Además, se aplica para calcular el excedente del consumidor y del productor, analizando las áreas entre las curvas de demanda y oferta.
Ejemplo
Supongamos que se desea encontrar el área entre la curva \( y = x^2 \) y el eje \( x \) desde \( x = 0 \) hasta \( x = 2 \). Esto se calcula como:
= = 4.2.1 Análisis de demanda y oferta
El análisis de demanda y oferta es un componente crucial de la economía y la administración de negocios, y el uso de integrales permite una comprensión más profunda de estos conceptos, particularmente en el cálculo de excedentes y el análisis de elasticidades.
Las funciones de demanda y oferta representan la relación entre el precio de un bien y la cantidad demandada u ofrecida.
Matemáticamente, estas funciones se expresan como:
- Función de demanda:
d
= D ( p ) - Función de oferta:
, s= S ( p )
Donde
Q d yQ s son las cantidades demandadas y ofrecidas, respectivamente, yp es el precio del bien. Estas funciones suelen ser decrecientes para la demanda y crecientes para la oferta (Martínez & Torres, 2019).Los conceptos de excedente del consumidor y del productor son fundamentales para medir el bienestar económico. Estos excedentes se pueden calcular utilizando integrales para encontrar las áreas entre las curvas de demanda y oferta y el precio de equilibrio.
Excedente del consumidor: Es la diferencia entre lo que los consumidores están dispuestos a pagar y lo que realmente pagan. Se calcula como:
"EC" =
- p eQ eDonde
D ( q ) es la función de demanda,p e es el precio de equilibrio, yQ e es la cantidad de equilibrio.Excedente del productor: Es la diferencia entre lo que los productores reciben y el costo de producción. Se calcula como:
"EP" = e
Q e- ∫ 0 Q e S ( q ) d q Donde
S ( q ) es la función de oferta (Gómez & López, 2020).La elasticidad mide la sensibilidad de la cantidad demandada u ofrecida ante cambios en el precio. La elasticidad precio de la demanda, por ejemplo, se calcula como:
\text{E_d} = \frac{dQ_d}{dp} \cdot \frac{p}{Q_d}
La integral puede utilizarse para calcular el cambio en el excedente del consumidor o del productor debido a cambios en la elasticidad de la demanda o la oferta.
El análisis de integrales en demanda y oferta es esencial para la toma de decisiones en políticas económicas y estrategias empresariales. Por ejemplo, los gobiernos pueden utilizar estos cálculos para evaluar el impacto de los impuestos o subsidios en el bienestar social (Rodríguez & Sánchez, 2021).
4.2.2 Cálculo de producción total y valor presente netos y cálculo de recursos
En economía y administración de negocios, el cálculo de la producción total, el valor presente neto (VPN) y el cálculo de recursos son herramientas esenciales para la evaluación y gestión de proyectos, así como para la toma de decisiones estratégicas. Estos conceptos permiten a las empresas y organizaciones evaluar la viabilidad y rentabilidad de inversiones, así como gestionar eficientemente los recursos disponibles.
El cálculo de la producción total se refiere a la cantidad total de bienes o servicios producidos en un período de tiempo determinado. Esto se puede analizar mediante la función de producción, que muestra la relación entre los insumos utilizados y la producción obtenida. Matemáticamente, una función de producción se puede expresar como:
Q=f(L,K)
donde Q es la producción total, L representa el trabajo, y K el capital. El análisis de esta función permite identificar cómo los cambios en los insumos afectan la producción total y cómo se pueden optimizar los procesos productivos (González & López, 2019).
El Valor Presente Neto (VPN) es una medida utilizada para evaluar la rentabilidad de una inversión o proyecto. Se calcula descontando los flujos de caja futuros al valor presente, utilizando una tasa de descuento que refleja el costo de oportunidad del capital. La fórmula del VPN es:
t( 1 + r ) t - C 0
donde Ft son los flujos de caja en el tiempo t, r es la tasa de descuento, n es el número de periodos, y 0 es la inversión inicial. Un VPN positivo indica que el proyecto es rentable, mientras que un VPN negativo sugiere que no lo es (Martínez & Pérez, 2020).
El cálculo de recursos implica la evaluación y asignación de los recursos necesarios para llevar a cabo un proyecto o actividad económica. Incluye el análisis de recursos financieros, humanos, materiales y tecnológicos. La optimización de recursos busca minimizar costos y maximizar la eficiencia en el uso de estos recursos.
- Análisis de costo-beneficio: Este análisis se utiliza para comparar los costos totales de un proyecto con los beneficios que se esperan obtener. Es fundamental para tomar decisiones de inversión y para la planificación de proyectos.
- Planificación de recursos: Involucra la identificación de los recursos necesarios, la programación de su uso y la gestión de cualquier limitación o restricción.
Ejemplo práctico
Supongamos que una empresa está considerando un proyecto con una inversión inicial de $100,000 y se espera que genere flujos de caja de $30,000 anuales durante 5 años. Con una tasa de descuento del 5%, el Valor Presente Neto (VPN) del proyecto se calcula para determinar su viabilidad.
-
Actividades
-
Ver Hacer un envío
-
Ver Hacer un envío
-
-
-
-
-
Introducción
L
a optimización de precios y producción es un aspecto crucial en la gestión de negocios y la economía. Implica el uso de técnicas matemáticas y análisis para determinar los niveles óptimos de precios y cantidades de producción que maximicen el beneficio de una empresa.
A continuación, se exploran estos conceptos y sus aplicaciones.
-
5.1 Optimización5.2 Funciones matemáticas en aplicaciones prácticas
La optimización de precios y producción es un aspecto crucial en la gestión de negocios y la economía. Implica el uso de técnicas matemáticas y análisis para determinar los niveles óptimos de precios y cantidades de producción que maximicen el beneficio de una empresa.
A continuación, se exploran estos conceptos y sus aplicaciones.
5.1.1 Optimización de precios
La optimización de precios se refiere a la determinación del precio ideal de un producto o servicio que maximiza los beneficios de la empresa. Esto se logra considerando diversos factores, como los costos de producción, la demanda del mercado, la competencia y la percepción del valor por parte de los consumidores.
Función de Demanda: Es esencial comprender cómo varía la demanda de un producto en función del precio. La función de demanda,
,
relaciona la cantidad demandada con el precio .
La elasticidad-precio de la demanda, que mide la sensibilidad de la demanda ante cambios en el precio, es crucial para la fijación de precios.
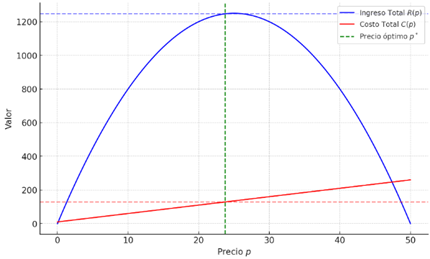
Figura 1: Maximización de beneficios
El gráfico muestra las funciones de ingreso total R(p) y costo total C(p) en función del precio p.Maximización del beneficio: El beneficio se maximiza cuando la derivada de la función de ingreso total menos la función de costo total con respecto al precio es igual a cero.
Matemáticamente, esto se expresa como:
Dondees el ingreso total y C(p) es el costo total (Pérez & Gómez, 2019).
La línea vertical verde punteada indica el precio óptimo p∗, donde la diferencia entre el ingreso total y el costo total (es decir, el beneficio) es máxima. Este punto se determina cuando la derivada del beneficio con respecto al precio es igual a cero, lo que significa que el ingreso marginal es igual al costo marginal en ese punto.
5.1.2 Optimización de la producción
La optimización de la producción implica determinar el nivel de producción que maximiza el beneficio o minimiza los costos. Esto se logra mediante el análisis de los costos marginales y los beneficios marginales.
- Costo marginal (CM): Es el costo de producir una unidad adicional. Se define como la derivada del costo total con respecto a la cantidad producida:
- Ingreso marginal (IM): Es el ingreso adicional obtenido por vender una unidad más de producto. Se calcula como la derivada del ingreso total con respecto a la cantidad vendida:
La regla para maximizar el beneficio es producir hasta el punto en que el ingreso marginal sea igual al costo marginal, es decir, IM=CM. Esto asegura que el costo de producir una unidad más no exceda el ingreso que genera (López & Torres, 2020).
En la práctica, la optimización de precios y producción se aplica en la fijación de precios de productos nuevos, en ajustes de precios en respuesta a cambios en el mercado y en la planificación de la capacidad de producción.
Por ejemplo, una empresa que fabrica dispositivos electrónicos puede usar estos principios para determinar cuántas unidades producir y a qué precio vender para maximizar los beneficios en diferentes regiones del mercado (Rodríguez & Sánchez, 2021).
En esta sección, revisaremos de manera simplificada las funciones que serán objeto de estudio en nuestra materia. Las funciones matemáticas son fundamentales en diversas áreas y se expresan mediante ecuaciones que relacionan variables.
Una función se define cuando a cada valor de entrada (generalmente x) le corresponde un valor de salida único (generalmente y). Gráficamente, una función es la representación visual de una ecuación.
Si una ecuación produce más de una salida para cada entrada, no define una función. Podemos imaginar una función como una "caja" que transforma una entrada en una salida específica.
Ejemplo de función
Considerando la ecuación:
4y−3x=8
Para definir y en función de x, despejamos:
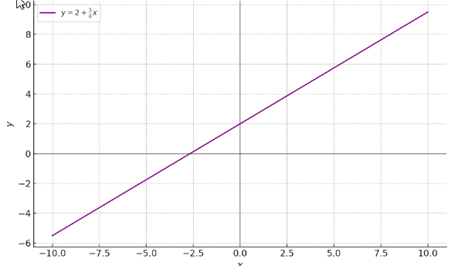
Figura 2: Gráfica de la función 𝑦=2+3/4𝑥
La pendiente positiva indica que la función crece a medida que x aumenta.Ejemplo de no función
Si tenemos:
Despejando y:
Aquí, y puede tomar dos valores para un mismo valor de x, por lo que no es una función.
Prueba gráfica
Para verificar si una ecuación es una función, utilizamos la prueba de la línea vertical. Si al trazar una línea vertical sobre la gráfica de la ecuación, esta intersecta la gráfica en más de un punto, entonces la ecuación no define una función.
Dominio de una función
El dominio de una función son los valores de x para los cuales la función está definida. Por ejemplo, para la función:
La expresión dentro de la raíz debe ser mayor o igual a cero:
El dominio de esta función es:
Aplicaciones en negocios
En el contexto de los negocios, se utilizan funciones específicas como las de costo, precio-demanda, ingresos y lucro.
Función de costo
C(x)=a+bx- a es el costo fijo.
- bx es el costo variable.
Función precio-demanda
P(x)=m-nxx es el número de ítems vendidos.
Función de ingresos
R(x)=x⋅P(x)- P(x) es la función de precio-demanda.
- R(x) es el ingreso total, que es el número de ítems vendidos por el precio de cada ítem.
Función de lucro
L(x)=R(x)-C(x)- L(x) es el lucro, que es la diferencia entre los ingresos y los costos.
Ejemplo práctico
Consideremos la función precio-demanda:
P(x)=75-3x
donde x está entre 1 y 20.
Para calcular los ingresos (R(x)):Completar una tabla de ingresos
Si vendemos x millones de ítems, los ingresos se calculan como:
- Para x=1:
- Para x=4:
- Y así sucesivamente hasta x=20.
Las funciones matemáticas son herramientas esenciales para analizar y resolver problemas en diversas áreas, incluidas las de los negocios.
- Costo marginal (CM): Es el costo de producir una unidad adicional. Se define como la derivada del costo total con respecto a la cantidad producida:
-
Profundiza más
Este video te ayudará a enfatizar sobre Funciones de Negocios ¡Accede aquí!
-
Actividades
-
-
-
Introducción
E
El modelado matemático y geométrico es una herramienta esencial en la enseñanza y práctica de las matemáticas y otras ciencias. Herramientas como GeoGebra y diversos simuladores ofrecen plataformas poderosas para visualizar y manipular modelos matemáticos, facilitando la comprensión y resolución de problemas complejos.
En esta sección se presentará un ejemplo práctico de cómo graficar funciones utilizando GeoGebra, una herramienta muy útil para visualizar conceptos matemáticos.
-
6.1 Modelado con ayuda de herramientas como GeoGebra o Simuladores
6.1.1 Utilizando GeoGebra
GeoGebra es un software de matemáticas dinámicas que combina geometría, álgebra, cálculo y estadísticas en una sola plataforma. Es especialmente útil para estudiantes y educadores debido a sus características interactivas y su capacidad para visualizar conceptos abstractos. Entre sus aplicaciones se incluyen:
- Geometría dinámica: Permite la construcción y manipulación de figuras geométricas, facilitando la comprensión de propiedades geométricas y teoremas. Por ejemplo, se pueden explorar las propiedades de los triángulos y sus circuncentros, incentros, etc. (Gómez & Rodríguez, 2019).
- Álgebra y cálculo: GeoGebra soporta la manipulación algebraica y el análisis de funciones. Es posible graficar funciones, encontrar intersecciones, calcular derivadas e integrales, y explorar el comportamiento de las funciones mediante la modificación de parámetros.
- Estadísticas y probabilidades: Ofrece herramientas para el análisis de datos y la visualización de distribuciones de probabilidad, lo cual es útil en estadística descriptiva e inferencial.
Se recomienda utilizar GeoGebra Clásico para estas actividades. Al abrir GeoGebra, aparecerá una interfaz donde se podrán ingresar funciones y visualizar sus gráficas.
Ejemplo de función ingreso
Recordar que una de las funciones que se visualizó anteriormente:
Para graficarla en GeoGebra, deben seguir estos pasos:
- Ingresen la función en el campo de entrada como:
- Inmediatamente, GeoGebra mostrará la gráfica de esta función en el plano cartesiano.
Pueden ajustar los ejes y hacer zoom para una mejor visualización de la curva.
Ejemplo de función de costo y ganancia
Supongamos que el departamento financiero de una compañía establece la siguiente función de costo para producir y vender x miles de laptops: donde los costos están en miles de dólares.
Función de ganancia
Para calcular la función de ganancia, primero necesitamos definir la función de ingresos.
Supongamos que la función precio-demanda es:
y que está entre 1 y 25 (miles de laptops).
La función de ingresos se calcula como:
La función de ganancia es la diferencia entre los ingresos y los costos:
La función de ganancia
Agrupamos términos semejantes:
Graficar la función de ganancia
Para graficar la función de ganancia en GeoGebra:
Ingresen la función de ganancia en el campo de entrada como:
La gráfica mostrará la parábola correspondiente a esta función.
Análisis de la gráfica
Al observar la gráfica, notarán que:
- La parábola puede tener puntos donde la ganancia es negativa, lo que indica que los costos superan los ingresos.
- La parábola también tendrá un punto máximo, que es donde la ganancia es mayor.
Punto de quiebre (punto de equilibrio)
El punto de quiebre es el punto donde los ingresos igualan los costos. En otras palabras, es donde .
Este punto se puede encontrar resolviendo la ecuación cuadrática:
En GeoGebra, pueden encontrar este punto utilizando la herramienta de intersección para ver dónde la gráfica de cruza el eje x.
Ejercicio adicional
El departamento de marketing de una empresa que fabrica y vende chips de memoria establece las siguientes funciones:
- Ingreso: R(x)=...
- Costo: C(x)=...
Donde x representa la cantidad de unidades vendidas, en el rango de 1,000 a 25,000.
- Realicen la resta de las funciones de ingresos y costos para obtener la función de ganancia.
- Grafiquen ambas funciones y encuentren los puntos de quiebre.
- Utilicen GeoGebra para visualizar estos puntos y analizar los resultados.
El uso de GeoGebra facilita la comprensión y visualización de las funciones matemáticas aplicadas a situaciones prácticas, como el análisis de ganancias en los negocios.
6.1.2 Visualización y análisis de las funciones matemáticas aplicadas a negocios
En esta sección, se continúa con el ejercicio pendiente sobre la graficación de las funciones de ingreso y costo utilizando GeoGebra. Este análisis permitirá entender mejor los puntos de quiebre y cómo determinar la cantidad óptima de producción para maximizar las ganancias.
Graficación de la función de ingreso
Primero, se grafica la función de ingreso que se tiene: R(x)=x*(75−3x)
Para graficarla en GeoGebra:
- Ingresen la función en el campo de entrada como: R(x)=75x−3x2
- Presionen "Enter" para visualizar la gráfica.
Verán que la gráfica de esta función es una parábola.
Graficación de la función de costo
Ahora, se grafica la función de costo: C(x)=125+16x
Para graficarla en GeoGebra:
- Ingresen la función en el campo de entrada como: C(x)=125+16x
- Presionen "Enter" para visualizar la gráfica.
La gráfica de la función de costo es una línea recta.
Puntos de intersección y puntos de quiebre
Para encontrar los puntos de intersección entre la función de ingreso y la función de costo:
- Utilicen la herramienta de "Punto" en GeoGebra.
- Hagan clic en los puntos donde las dos gráficas se cruzan.
Por ejemplo, uno de los puntos de intersección puede ser: (17.25,401.02)
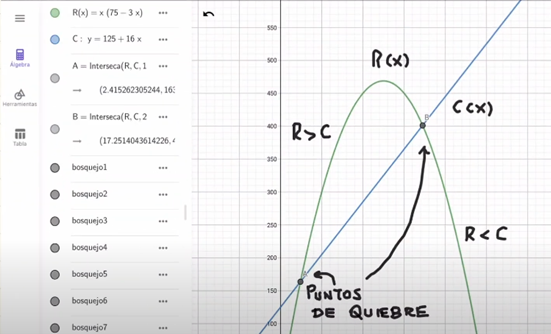
Figura 3: Puntos de quiebre
Esto significa que al vender 17.25 miles de unidades, tanto el ingreso como el costo son 401.02 miles de dólares.Análisis de los puntos de quiebre
Los puntos de quiebre son cruciales para entender cuándo los ingresos igualan a los costos. En otras palabras, son los puntos donde R(x)=C(x). En este ejercicio, se encuentra que los puntos de quiebre están aproximadamente en: (2.42,163.64) (17.25,401.02)
Interpretación de la gráfica
La gráfica muestra que:
- Para x < 2.42, los ingresos son menores que los costos, resultando en una pérdida.
- Para 2.42 < x < 17.25, los ingresos superan a los costos, generando una ganancia.
- Para x > 17.25, nuevamente los ingresos son menores que los costos, resultando en una pérdida.
Esto indica que la producción óptima para maximizar las ganancias está entre 2.42 y 17.25 miles de unidades.
Este tipo de análisis es fundamental para cualquier empresario o persona que gestione un negocio. Saber cuántas unidades producir para maximizar las ganancias puede marcar la diferencia entre un negocio rentable y uno no rentable.
Por ejemplo, si un fabricante de laptops quiere maximizar sus ganancias, debería producir entre 2,420 y 17,250 unidades, según el análisis de las funciones de ingreso y costo.
El análisis de funciones cuadráticas y lineales, así como la identificación de los puntos de quiebre, son herramientas poderosas en la matemática aplicada a los negocios. Estas herramientas permiten tomar decisiones informadas sobre la producción y las ventas para maximizar las ganancias.
-
Profundiza más
Este video te ayudará a enfatizar sobre Ejemplos de Geogebra ¡Accede aquí!
Profundiza más
Este video te ayudará a enfatizar sobre Puntos de Corte ¡Accede aquí!
-
-
Uso de herramientas de cálculo diferencial e integral para visualización de costos, lucros e ingresos y cantidades marginales
-
Introducción
L
as funciones racionales son aquellas que se expresan como el cociente de dos polinomios.
Un ejemplo de función racional es:
En estas funciones, una característica importante son las asíntotas. Una asíntota es una línea a la cual la función tiende a aproximarse, pero nunca alcanza.
-
7.1 Uso de herramientas de cálculo diferencial e integral para visualización de costos, lucros e ingresos y cantidades marginales
Es la línea recta a la que una función se aproxima cada vez más a medida que la variable independiente tiende hacia el infinito o hacia un punto específico, pero que nunca llega a tocar.
Para visualizar esta definición, considere el siguiente gráfico de la función utilizando Python.
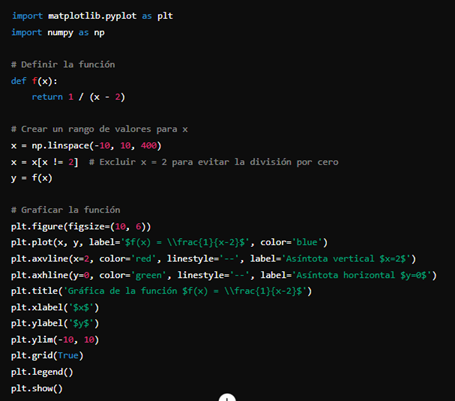
Figura 4: Gráfica de la función utilizando Python
Las asíntotas pueden ser verticales, horizontales u oblicuas, dependiendo de la naturaleza de la función y su comportamiento a largo plazo (Stewart, 2018).7.1.1 Tipos de asíntotas
Existen tres tipos principales de asíntotas:
Asíntotas verticales: Ocurren cuando el denominador de la función se iguala a cero y el numerador no se anula en esos puntos.
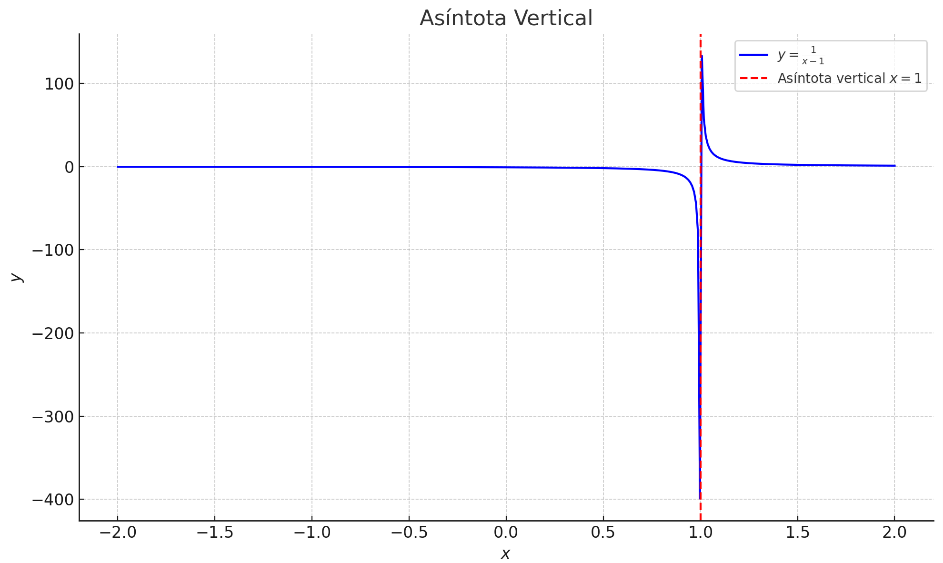
Figura 5: Asíntotas verticales
Gráfica extraída de GeogebraAsíntotas horizontales: Se determinan por el comportamiento de la función cuando x tiende al infinito.
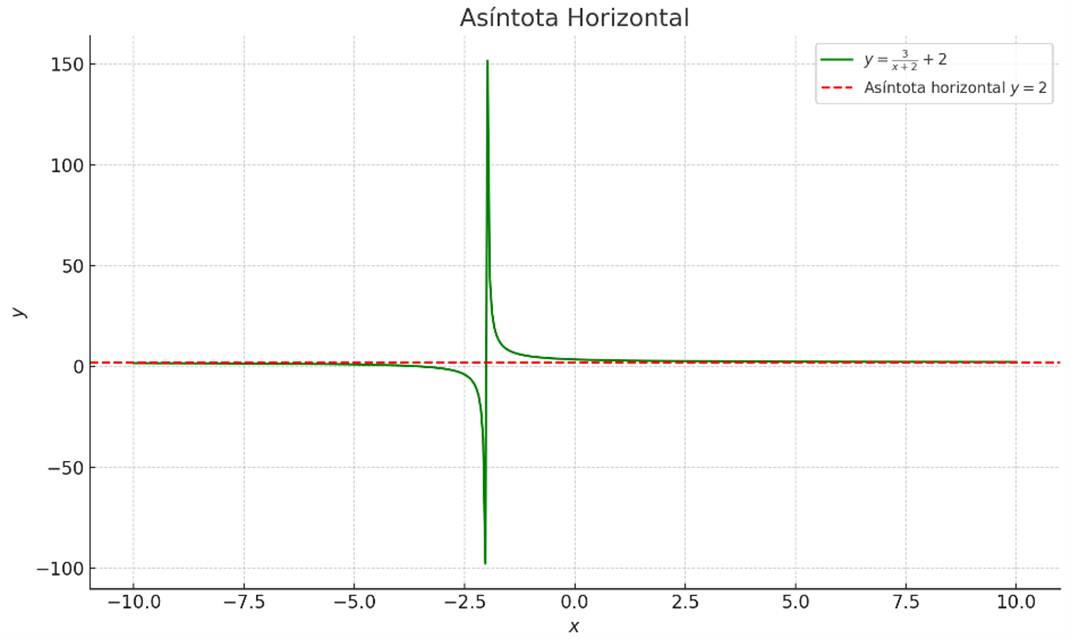
Figura 6: Asíntota Horizontal
Gráfica extraída de GeogebraAsíntotas inclinadas: Ocurren cuando el grado del numerador es mayor que el grado del denominador.
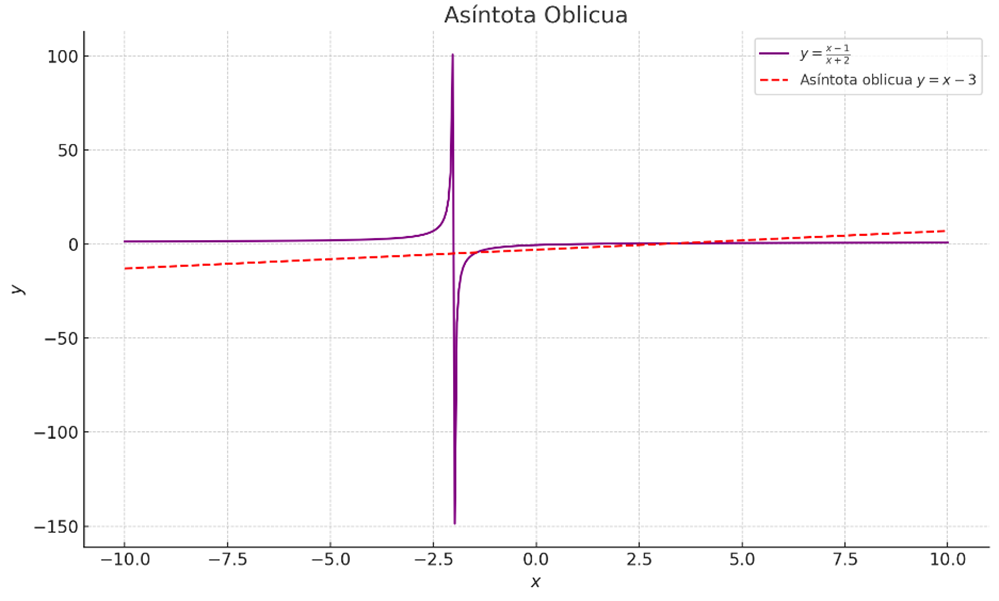
Figura 7: Asíntota oblicua
Gráfica extraída de GeogebraDeterminación de asíntotas
Para encontrar las asíntotas verticales, se iguala el denominador a cero y se resuelve para x. Si: entonces x = c es una asíntota vertical.
Para encontrar las asíntotas horizontales, se comparan los grados del numerador y del denominador:
- Si el grado del numerador es menor que el grado del denominador , entonces es la asíntota horizontal.
- Si los grados son iguales, la asíntota horizontal es: , donde y son los coeficientes principales de y , respectivamente.
- Si el grado del numerador es mayor que el grado del denominador, no existe asíntota horizontal.
La aplicación en negocios se puede ilustrar con un ejemplo. Supongamos que una compañía fabrica tablas de nieve con costos fijos de $200 por día y costos totales de $3800 por día al producir 20 tablas.
La función de costo es:
La función de costo promedio se define como:
Gráfico del costo promedio
Al graficar la función de costo promedio, se pueden determinar las asíntotas:
- Asíntota vertical: Se presenta en x = 0, ya que la función se indetermina en ese punto.
- Asíntota horizontal: Es y = 180, ya que, al dividir el coeficiente principal del numerador por el del denominador, se obtiene 180.
La asíntota horizontal en y = 180 indica que, a medida que la producción aumenta, el costo promedio por tabla tiende a ser $180.
Esto es crucial para entender que, aunque la producción se incremente significativamente, el costo promedio no superará los $180 por tabla.
Aquí tienes el texto corregido:
Ejercicio de aplicación
Supongamos una compañía fábrica tablas de nieve con los siguientes datos:
- Costos fijos: $200 por día.
- Costos totales: $3800 por día para 20 tablas.
- Función de costo:
- Función de costo promedio:
- Gráfico del costo promedio:
- Asíntota vertical: x=0
- Asíntota horizontal: y =180
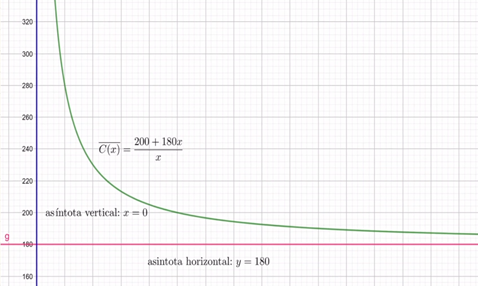
Figura 8: Gráfica del ejemplo
Las asíntotas en funciones racionales son fundamentales para entender el comportamiento a largo plazo de las funciones aplicadas en los negocios.En el caso del costo promedio de fabricación, sabemos que, al incrementar la producción, el costo promedio se estabilizará en $180 por tabla, lo que proporciona una guía importante para la toma de decisiones en producción y ventas.
-
Profundiza más
Este video te ayudará a enfatizar sobre Costo Promedio ¡Accede aquí!
-
-
-
Introducción
E
n el ámbito de los negocios, la toma de decisiones informada se basa en un análisis preciso y una visualización efectiva de los datos. Las herramientas de cálculo, como GeoGebra y Wolfram Alpha, facilitan este proceso al proporcionar representaciones numéricas y visuales claras de los modelos matemáticos.
-
8.1 Forma de obtener resultados en situaciones reales de negocios
Estas herramientas son especialmente útiles para situaciones complejas que requieren un análisis detallado, y permiten una comparación directa con los cálculos realizados manualmente (Stewart, 2018).
Aquí tienes algunas recomendaciones para obtener situaciones reales de negocios:
- Identificar el problema o la decisión que necesita ser tomada, como determinar el precio óptimo de un producto para maximizar los beneficios.
- Recopilar todos los datos relevantes que afectarán el análisis, como los costos de producción, la demanda del mercado, los precios de la competencia, entre otros.
- Elegir las funciones matemáticas que mejor representen la situación, por ejemplo, usar una función de costo y una función de ingreso para modelar los beneficios.
- Utilizar herramientas como GeoGebra y Wolfram Alpha para realizar cálculos y visualizar los resultados. Estas herramientas ofrecen gráficos interactivos y resultados numéricos precisos que facilitan la comprensión.
- Realizar los mismos cálculos manualmente para verificar la precisión de los resultados obtenidos con las herramientas digitales.
- Analizar los resultados obtenidos y usar esta información para tomar decisiones informadas que optimicen los objetivos de negocio.
Wolfram Alpha es una plataforma de computación basada en la web que proporciona respuestas a preguntas formuladas en lenguaje natural mediante el uso de algoritmos avanzados y una vasta base de datos de conocimiento. Es especialmente útil en el campo del cálculo, ya que permite realizar cálculos simbólicos y numéricos, generar gráficos y ofrecer soluciones paso a paso para problemas complejos.
8.1.1 Uso de GeoGebra y Wólfram Alpha para visualización de resultados numéricos y visuales de cálculo aplicado a negocios con ejemplos y comparación con resultados hechos a mano
Vamos a explorar cómo utilizar una herramienta muy poderosa para resolver ecuaciones: Wolfram Alpha. Esta aplicación emplea inteligencia artificial para resolver problemas matemáticos y ofrece una amplia gama de aplicaciones que van más allá de las matemáticas.

Figura 9: Página principal de Wolfram Alpha
Wolfram Alpha muestra en su página principal las diferentes opcionesWolfram Alpha no solo se limita a resolver ecuaciones matemáticas, sino que también tiene aplicaciones en diversas áreas, como:
- Álgebra
- Cálculo
- Geometría
- Ecuaciones diferenciales
- Estadística
Además, se puede utilizar en campos como la física, las ciencias computacionales, las ciencias de la Tierra, así como en áreas como finanzas, historia y cultura.
Ejemplo práctico
Vamos a usar Wolfram Alpha para resolver un sistema de ecuaciones que vimos en el video anterior. A continuación, se presentan los pasos:
Primera ecuación:
3x−10=2y−1
En Wolfram Alpha, cuando hay multiplicación, se usa el asterisco (*). Entonces se escribe:
3∗x−10=2∗y−1
Segunda ecuación:
5y+2x=7
Ingresar las ecuaciones en Wolfram Alpha:
- Las ecuaciones deben separarse con una coma.
- Si hay más de dos ecuaciones, pueden separarse con punto y coma.
- Ingresamos las ecuaciones en Wolfram Alpha como:
3∗x−10=2∗y−1,5∗y+2∗x=7
Resultados
Al calcular, Wolfram Alpha nos proporcionará los resultados. En este caso, obtuvimos:
x=5919
y=319Estos resultados coinciden con los que obtuvimos manualmente en el ejercicio anterior. Para un mejor aprendizaje, es recomendable resolver primero el sistema de ecuaciones manualmente y luego utilizar Wolfram Alpha para verificar los resultados. Si los resultados no coinciden, revisen su resolución para identificar y corregir cualquier error.
Beneficios de Wolfram Alpha
Wolfram Alpha, al utilizar inteligencia artificial, ofrece soluciones rápidas y precisas, lo cual es de gran ayuda para verificar el trabajo manual. Esto permite identificar posibles errores en el proceso de resolución y aprender de ellos. Es una herramienta valiosa que puede mejorar significativamente el aprendizaje y la comprensión de las matemáticas.
Funcionalidades de Wolfram Alpha en el cálculo
Wolfram Alpha permite:- Calcular derivadas e integrales de funciones simples y complejas, lo que incluye derivadas parciales y múltiples, así como integrales definidas e indefinidas.
- Evaluar límites de funciones y series infinitas, lo cual es útil para analizar el comportamiento de las funciones cerca de puntos específicos y para estudiar la convergencia de series.
- Resolver ecuaciones diferenciales ordinarias (ODEs) y parciales (PDEs), proporcionando soluciones generales y particulares.
- Generar gráficos de funciones en 2D y 3D, lo cual es esencial para la visualización de curvas, superficies y soluciones de ecuaciones.
Utilizando Wolfram Alpha, las empresas pueden optimizar funciones de costos y beneficios al encontrar derivadas e identificar puntos críticos. Por ejemplo, para maximizar el beneficio se puede calcular la derivada y encontrar los puntos donde la derivada es cero.
Wolfram Alpha también puede ayudar a analizar funciones de demanda y oferta, calcular elasticidades y evaluar el impacto de cambios en variables económicas. Un ejemplo sería analizar la función de demanda , y calcular la elasticidad precio de la demanda en varios puntos.
Profesores y estudiantes pueden utilizar Wolfram Alpha para verificar resultados y comprender mejor los conceptos a través de visualizaciones y explicaciones detalladas. Por ejemplo, al estudiar integrales definidas, los estudiantes pueden usar Wolfram Alpha para verificar sus respuestas y ver los gráficos correspondientes a las áreas bajo las curvas.
Wolfram Alpha es una herramienta poderosa y versátil que facilita la resolución de problemas complejos en cálculo. Su capacidad para realizar cálculos precisos, proporcionar soluciones detalladas y generar visualizaciones claras la convierte en un recurso invaluable tanto en entornos educativos como profesionales.
-
Profundiza más
Este video te ayudará a enfatizar sobre el uso de Wolfram Alpha ¡Accede aquí!
-
Actividades de refuerzo
-
Ver Hacer un envío
-
-
-
-
Introducción
En esta sesión, haremos una pausa para explicar el programa que utilizaremos en este curso: Python. Aprenderemos cómo instalarlo y cómo utilizar Google Colab como una herramienta alternativa para aquellos que prefieren no instalar Python en sus computadoras.
-
9.1. Instalación de Python9.2 Uso de Google Colab
Para comenzar, abrimos nuestro buscador favorito y escribimos "". El primer resultado será la página oficial: python.org. Allí encontraremos todo lo necesario para descargar e instalar Python, así como tutoriales y documentación oficial.
Figura 10
Página principal de Python
Figura 1: Prueba de Imagen Nota. Desde este sitio oficial podrá descargar y revisar la documentación de Python.
Pasos para la instalación
Acceder a la página oficial: Ingresamos a python.org.
Descargar Python: En la sección de descargas, seleccionamos la versión adecuada para nuestro sistema operativo (Windows, macOS, Linux, etc.).
Seguir las instrucciones de instalación: Dependiendo del sistema operativo, seguimos las instrucciones para completar la instalación.
Es importante señalar que las versiones más recientes de Python pueden no ser compatibles con sistemas operativos antiguos, como Windows 7. En ese caso, se recomienda instalar una versión anterior de Python.
9.3 Python aplicado a Negocios con CálculoPara aquellos que prefieren no instalar Python en su computadora, Google ofrece una excelente alternativa: . Esta herramienta permite ejecutar código Python directamente en el navegador, sin necesidad de instalaciones adicionales.
Acceso a Google Colab
- Abrir una nueva pestaña en el navegador: Escribimos "Google Colab" en el buscador.
- Acceder a la página de Google Colab: Ingresamos al primer resultado, que será la página oficial de Google Colab.
- Iniciar sesión con una cuenta de Google: Para utilizar Google Colab, necesitamos una cuenta de Gmail.
- Google Colab permite crear y compartir cuadernos que contienen código Python, texto explicativo, imágenes y más. Todos los proyectos se guardan en Google Drive, facilitando la colaboración y el acceso desde cualquier dispositivo.
Beneficios de Google Colab
- No requiere instalación: Todo se ejecuta en la nube.
- Acceso a recursos avanzados: Podemos utilizar GPU (unidad de procesamiento gráfico) para tareas que requieren gran capacidad de procesamiento.
- Facilidad de colaboración: Es posible compartir cuadernos con colegas y trabajar en proyectos de manera colaborativa.
Exploración de Google Colab
Al acceder a Google Colab, se puede ver una introducción que explica sus características y funcionalidades. Aquí, también se pueden ver ejemplos de uso en ciencia de datos, aprendizaje automático y más.
- Crear un nuevo cuaderno en Google Colab
- Crear un nuevo cuaderno: Hacemos clic en "Nuevo cuaderno".
- Iniciar sesión en Google: Si no hemos iniciado sesión, se nos pedirá hacerlo con nuestra cuenta de Gmail.
- Empezar a escribir código: Una vez dentro, podemos empezar a escribir y ejecutar código Python directamente en el cuaderno.
Para empezar a programar en Python, necesitas una cuenta de Gmail. Con esta cuenta, podrás acceder a Google Colab, una plataforma interactiva que te permitirá escribir y ejecutar código en Python directamente desde el navegador.
Acceder a Google Colab
- Abre el navegador y busca "Google Colab".
- Inicia un nuevo cuaderno (notebook): Esto te permitirá comenzar a escribir y ejecutar código en Python.
Figura 11
Pantalla principal de Google Colab
Figura 1: Prueba de Imagen Nota. Pantalla principal de la herramienta de Google Colab con todas las opciones
9.3.1 Comandos de Python básicos
A continuación, cubriremos algunos conceptos básicos necesarios para nuestros desafíos de programación.
Variables y tipos de datos
En Python, se pueden almacenar datos en variables. Estos datos pueden ser de diferentes tipos, como números, cadenas de caracteres (strings) o valores booleanos.
Ejemplos:
Figura 12
Ejemplo de variables y tipos
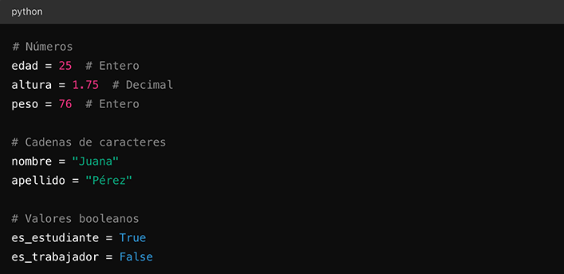
Figura 1: Prueba de Imagen Nota. Ingreso de cadena de caracteres y valores booleanos
Se puede usar el comando print para mostrar el valor de estas variables:
Figura 13
Comando print

Figura 1: Prueba de Imagen Nota. Código simple de comando print.
Listas
Las listas son colecciones ordenadas de elementos. Pueden contener diferentes tipos de datos.
Ejemplos:
Figura 14
Listas en Python
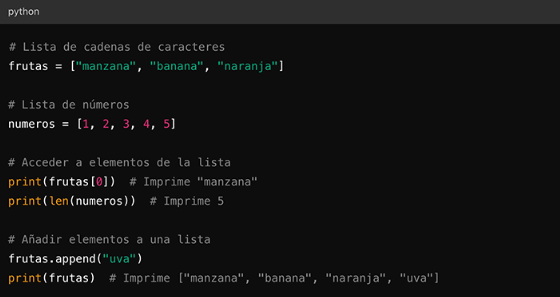
Figura 1: Prueba de Imagen Nota. Código en Python para listas
Operaciones Básicas
Python permite realizar operaciones aritméticas y comparaciones sencillas.
Figura 15
Operaciones aritméticas en Python
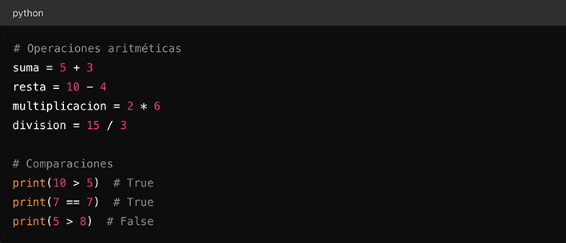
Figura 1: Prueba de Imagen Nota. Código para operaciones en Python.
Bucles
Los bucles se utilizan para repetir acciones. En Python, los dos tipos principales son: for y while.
Ejemplos:
Figura 16
Bucles en Python
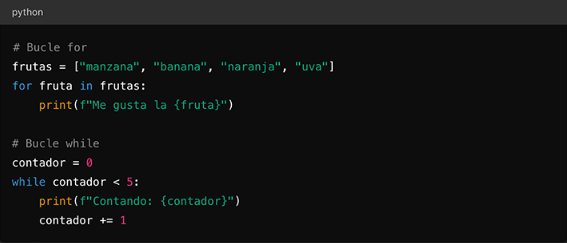
Figura 1: Prueba de Imagen Nota. Código simple para bucles en Python.
Google Colab
Es una herramienta basada en la nube que permite escribir y ejecutar código en Python directamente en el navegador. Proporciona acceso a recursos de computación gratuitos y facilita compartir y colaborar en proyectos, lo que potencia el aprendizaje y desarrollo de aplicaciones de datos y aprendizaje automático.
Python
Es un lenguaje de programación de alto nivel, interpretado y de propósito general, conocido por su sintaxis clara y legible. Es ampliamente utilizado en el desarrollo web, análisis de datos, inteligencia artificial, automatización de tareas, entre otros, gracias a su extensa biblioteca estándar y su activa comunidad de desarrolladores.
-
Profundiza más
Este video te ayudará a enfatizar sobre introducción a Google Colab ¡Accede aquí!
Profundiza más
Este video te ayudará a enfatizar sobre una introducción a Python ¡Accede aquí!
-
-
-
Introducción
H
oy vamos a aprender sobre NumPy, una librería esencial para la computación científica en Python. Veremos los conceptos básicos y cómo utilizarlos en nuestros proyectos.
-
10.1 Instalación y Configuración10.2 Operaciones básicas
Para usar , primero debemos importarla. Utilizaremos el siguiente comando:
Figura 17
Importación de librería NumPy

Código para importar librerías en NumPy Con esto, cada vez que queramos usar alguna función de NumPy, simplemente escribiremos np seguido de la función correspondiente.
10.3 Operaciones con ArraysCreación de Arrays
Los arrays son estructuras de datos fundamentales en NumPy. Veamos cómo crear y manipular arrays.
Creación de un Array Unidimensional
Podemos crear un array unidimensional (vector) de la siguiente manera:
Figura 18
Código para estructura de datos arrays

Creación de un código de array unidimensional Creación de una Matriz
Para crear una matriz (array bidimensional), es necesario definir las filas y las columnas:
Figura 19
Código para una matriz 2×3 en Python

Esto generará una matriz con dos filas y tres columnas. Si queremos una matriz de 3×3, añadimos una fila más:
Figura 20
Código para una matriz 3×3 en Python

Esto generará una matriz con tres filas y tres columnas. 10.4 Listas, diccionarios, dataframesNumPy permite realizar operaciones matemáticas entre arrays de manera eficiente.
Suma de Arrays
Podemos sumar dos arrays de la siguiente manera:
Figura 21
Suma de elementos en Python
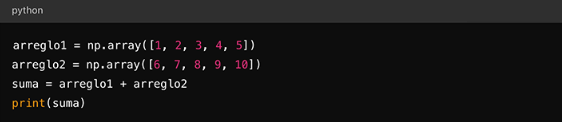
Esto sumará elemento por elemento de los dos arrays, resultando en un nuevo array [7, 9, 11, 13, 15]. Slicing (Subconjuntos de Arrays)
Podemos extraer subconjuntos de un array utilizando slicing. Por ejemplo, para obtener los elementos del segundo al cuarto:
Figura 22
Impresión de resultados

Esto imprimirá [2, 3, 4]. Funciones en NumPy
Las funciones nos permiten realizar operaciones repetitivas de manera más sencilla y eficiente.
Definición de una Función
Supongamos que queremos calcular el promedio de los elementos de un array. Podemos definir una función para hacerlo.
Figura 23
Código para promedio

Con esto se obtendrá el promedio de elementos en un array. Uso de la Función
Podemos usar esta función para calcular el promedio de diferentes arrays:
Figura 24
Promedio de diferentes arrays
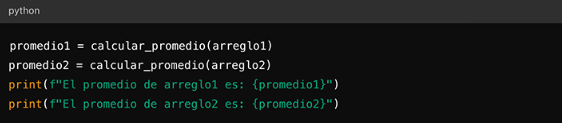
Se muestra el promedio de cada uno de los promedios. En esta sección se han revisado los siguientes temas:
- Cómo importar y configurar NumPy.
- Crear arrays unidimensionales y matrices.
- Realizar operaciones básicas con arrays.
- Extraer subconjuntos de arrays.
- Definir y utilizar funciones en NumPy.
Practiquen estos conceptos para familiarizarse con NumPy y sus capacidades.
Python es un lenguaje de programación ampliamente utilizado en el análisis de datos, el desarrollo web, la automatización y más. Entre las estructuras de datos fundamentales en Python se encuentran las listas, los diccionarios y los DataFrames, cada una con sus características y usos específicos.
10.4.1 Listas
Las listas en Python son estructuras de datos que permiten almacenar una colección ordenada y mutable de elementos. Los elementos de una lista pueden ser de cualquier tipo de dato. Se definen usando corchetes [] y se pueden modificar después de su creación.
- Indexación: Los elementos de una lista se pueden acceder mediante índices, empezando desde 0.
- Mutabilidad: Se pueden cambiar, agregar o eliminar elementos de una lista.
- Funciones y métodos: Python proporciona métodos como append(), remove(), sort(), len(), etc.
Ejemplo
Figura 25
Manipulación de listas

Se muestra código de función append. 10.4.2 Diccionarios
Los diccionarios son estructuras de datos que almacenan pares de clave-valor. Las claves deben ser únicas e inmutables. Se definen usando llaves {}.
- Acceso a valores: Los valores se acceden usando las claves asociadas.
- Mutabilidad: Se pueden agregar, modificar o eliminar pares de clave-valor.
- Funciones y métodos: Métodos como get(), keys(), values(), items(), etc.
Ejemplo
Figura 26
Código de diccionario

Código con estructura de diccionario basado en datos personales. 10.4.3 DataFrames
Los DataFrames, de la biblioteca pandas, son estructuras bidimensionales similares a tablas de base de datos o Excel. Son ideales para el análisis de datos.
- Indexación: Filas y columnas etiquetadas.
- Manipulación: Filtrado, agrupamiento, agregación y más.
- Integración: Pueden crearse desde CSV, bases de datos y otras fuentes.
Ejemplo
Figura 27
Estructura de pandas
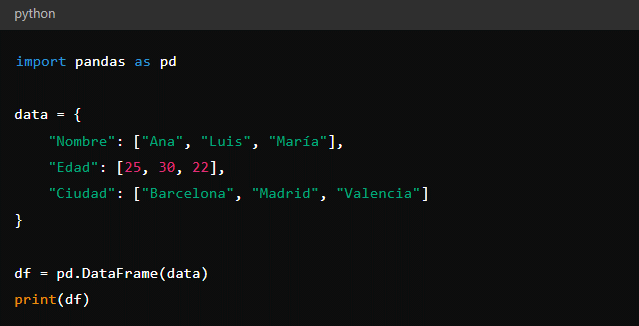
Ejemplo de pandas en Python. 10.4.4 Pandas y Matplotlib
En esta sección, veremos cómo aplicamos Python a las funciones de costo, precio, demanda, ingresos, lucro y puntos de quiebre que ya hemos estudiado teóricamente.
Usaremos NumPy y para visualizar funciones de costo, precio, demanda, ingreso y lucro.
Importación de Librerías
Primero, importamos las librerías necesarias:
Figura 28
Importación de NumPy y Matplotlib

NumPy para operaciones numéricas y Matplotlib para gráficos. Definición de funciones
Definimos las funciones que utilizaremos: costo, precio, demanda, ingreso y lucro. Recordemos que:
- Costo: Tiene una parte fija y una parte variable.
- Precio y demanda: Dependen de dos constantes, m y n, donde n se multiplica por x.
- Ingreso: Es x multiplicado por el precio de demanda.
- Lucro: Es la resta entre ingreso y costo.
- En todas estas funciones, x representa el número de ítems vendidos.
Ejemplo
Figura 29
Definición de funciones
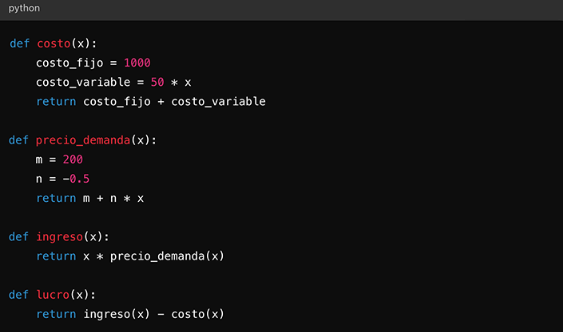
Definición de función costo en Python. Generación de datos
Usamos
np.linspacepara crear un vector de ítems vendidos.Figura 30
Generación de vectores

Rango continuo de datos para las funciones. Cálculo y visualización
Definimos nuestras variables para almacenar los valores de costo, precio, ingreso y lucro:
Figura 31
Definición de variables para funciones
Variables para la operación. Determinación del lucro máximo
Calculamos el número de ítems que debemos vender para obtener el máximo lucro:
Figura 32
Lucro máximo
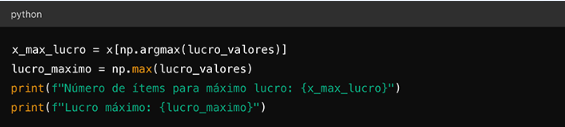
Punto de mayor beneficio. Puntos de equilibrio
Usamos una función para resolver ecuaciones y encontrar los puntos de quiebre:
Figura 33
Resolución de ecuaciones
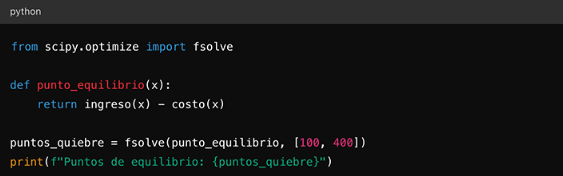
Código para punto de equilibrio. Visualización de resultados
Finalmente, visualizamos los resultados usando Matplotlib:
Figura 34
Visualización con Matplotlib
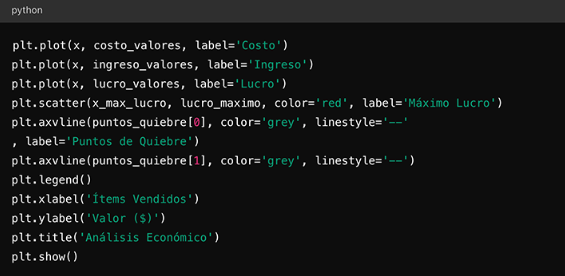
Ejemplo de resultados. Interpretación de los resultados
Costo (azul): Función lineal.
Ingreso (naranja): Función cuadrática.
Lucro (verde): Ingreso menos costo.
Máximo lucro (rojo): Punto de mayor beneficio.
Puntos de quiebre (gris): Rangos con lucro positivo.
Entre los quiebres se obtiene lucro positivo; fuera de ellos, no cubre el costo.
NumPy
Biblioteca fundamental para la computación científica en Python. Proporciona soporte para matrices y grandes conjuntos de datos multidimensionales, así como una colección de funciones matemáticas de alto nivel para operar con estos datos.
-
Profundiza más
Este video te ayudará a enfatizar sobre funciones en Numpy ¡Accede aquí!
Profundiza más
Este video te ayudará a enfatizar sobre Python aplicación, funciones, negocios ¡Accede aquí!
-
-
-
Introducción
L
a Programación Orientada a Objetos (POO) es un paradigma de programación que organiza el diseño del software alrededor de datos u "objetos", en lugar de funciones y lógica. Este enfoque facilita la creación de aplicaciones y sistemas más modularizados, reutilizables y manejables. En Python, la POO es ampliamente utilizada debido a su flexibilidad y simplicidad.
-
11.1 Conceptos fundamentales de la POO11.2 Ventajas de la POO
La POO se basa en cuatro conceptos fundamentales: clases, objetos, herencia y polimorfismo.
Clases y objetos
Una clase es una plantilla o modelo que define un conjunto de atributos y métodos que caracterizan a cualquier objeto de ese tipo. Los atributos representan los datos, mientras que los métodos representan el comportamiento.
Un objeto es una instancia de una clase. Cada objeto puede tener diferentes valores para los atributos definidos en su clase.
Ejemplo
Figura 35
Ejemplo de clase en Python
Ejemplo de una clase (coche) Herencia:
La herencia permite que una clase (subclase) herede atributos y métodos de otra clase (superclase), lo que facilita la reutilización del código y la creación de una jerarquía de clases.
Ejemplo:
Figura 36
Ejemplo de Herencia
En este ejemplo se muestra la creación de una superclase denominada vehículo. Polimorfismo:
El polimorfismo permite que diferentes clases utilicen la misma interfaz para métodos que pueden comportarse de manera diferente, lo que es fundamental para la flexibilidad y escalabilidad del código.
Figura 37
Ejemplo de poliformismo
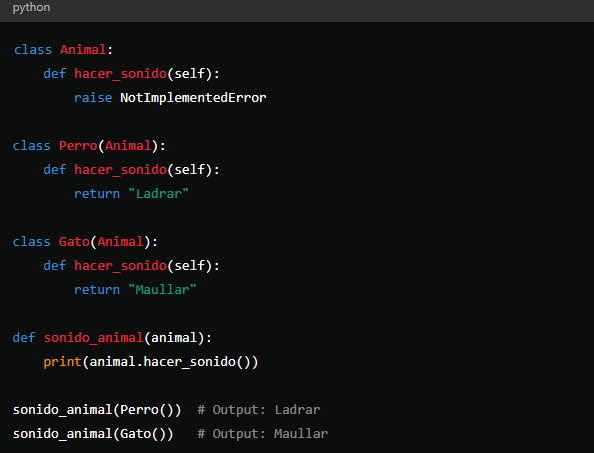
Se muestra un ejemplo de uso de diferentes interfaces para métodos 11.3 Funciones en PythonModularidad:
El código se organiza en módulos, lo que facilita su gestión y mantenimiento.
Reutilización:
A través de la herencia, se puede reutilizar código existente en nuevas aplicaciones.
Manejabilidad:
La POO facilita el trabajo en equipo, ya que el código es más comprensible y se pueden asignar módulos específicos a diferentes desarrolladores.
Escalabilidad:
Es más fácil ampliar sistemas existentes con nuevas características.
Python es un lenguaje altamente compatible con la POO. Su sintaxis simple y sus potentes bibliotecas lo hacen ideal para desarrollar aplicaciones de software que requieren una arquitectura basada en objetos, como juegos, aplicaciones de escritorio y sistemas complejos de procesamiento de datos (López & Torres, 2019).
11.4 Clases en Python y ejercicios de aplicaciónEn Python, las funciones son bloques de código reutilizables diseñados para realizar una tarea específica. Las funciones permiten la modularidad del código y mejoran la legibilidad y mantenibilidad de los programas. A continuación, se describen los conceptos fundamentales sobre las funciones en Python y se proporcionan ejemplos prácticos.
Una función en Python se define usando la palabra clave def, seguida del nombre de la función, paréntesis y un bloque de código indentado. Las funciones pueden aceptar argumentos y devolver valores.
Figura 38
Sintaxis básica
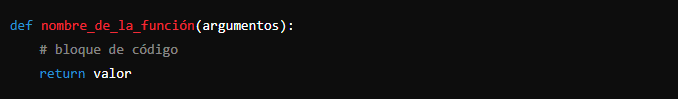
En la gráfica se muestra la sintaxis básica de funciones Las funciones pueden aceptar varios tipos de argumentos:
Argumentos posicionales:
Los valores se asignan a los parámetros en el orden en que se pasan.
Argumentos nombrados:
Los valores se asignan a los parámetros utilizando sus nombres.
Argumentos por defecto:
Los parámetros pueden tener valores por defecto que se utilizan si no se pasa un valor para ese parámetro.
Argumentos variables:
Se pueden usar para aceptar un número variable de argumentos (*args y **kwargs).
Figura 39
Ejemplo de argumentos
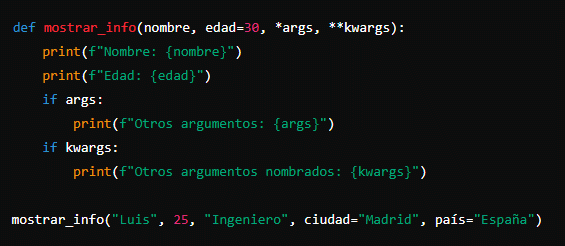
Código para declarar argumentos en Python Las funciones lambda, también conocidas como funciones anónimas, son funciones pequeñas y sin nombre definidas con la palabra clave lambda. Son útiles para realizar operaciones rápidas y simples.
Figura 40
Función lambda

Declaración de la función lambda Las funciones de orden superior son aquellas que aceptan otras funciones como argumentos o devuelven una función como resultado. Son fundamentales en la programación funcional.
Figura 41
Funciones de orden superior
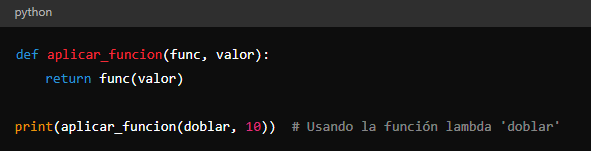
Ejemplo para aplicar funciones de orden superior Decoradores
Los decoradores son una forma de modificar el comportamiento de una función o método. Se definen como funciones que envuelven a otra función para extender su comportamiento.
Figura 42
Decoradores
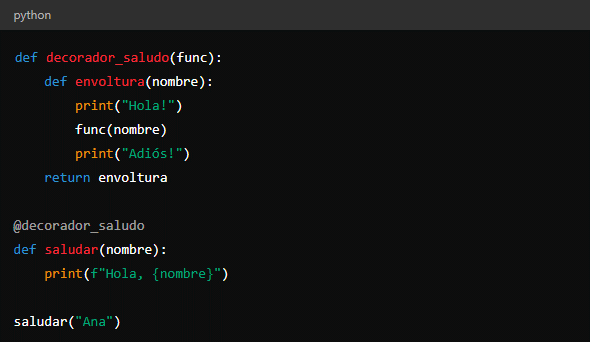
Ejemplo definición de decoradores en Python En el análisis de datos, las funciones se utilizan para limpiar, procesar y analizar grandes conjuntos de datos. Bibliotecas como pandas y numpy dependen en gran medida de las funciones para operar sobre estructuras de datos.
En el desarrollo web, las funciones se utilizan para manejar solicitudes y respuestas HTTP, procesar datos de formularios y generar contenido dinámico.
En Python, las clases son una de las características más importantes de la Programación Orientada a Objetos (POO). Las clases permiten crear nuevos tipos de objetos que agrupan datos y funcionalidades.
A continuación, se describen los conceptos fundamentales de las clases en Python, sus componentes y su uso en aplicaciones prácticas.
Una clase es una plantilla para crear objetos (instancias de clases). Los objetos son instancias concretas de las clases y representan entidades con propiedades y comportamientos definidos por la clase.
Figura 43
Ejemplo de Clase
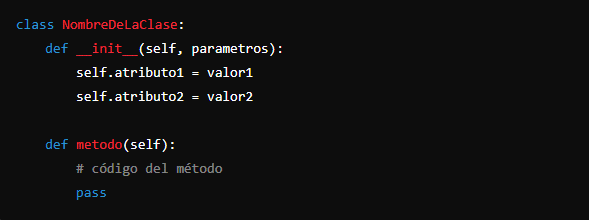
Ejemplo para practica de clases en Python Componentes de una clase
Método constructor
El método __init__ es el constructor de la clase y se llama automáticamente cuando se crea una nueva instancia. Inicializa los atributos del objeto.
Figura 44
Método constructor _init_
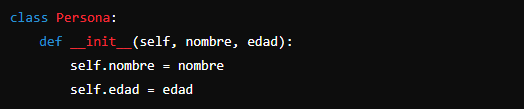
Ejemplo de definición de clase _init_ Atributos de Instancia:
Los atributos de instancia son variables que pertenecen a cada instancia de una clase. Se definen dentro del método constructor __init__.
Figura 45
Atributos de instancia
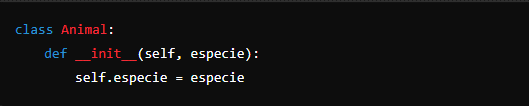
En el ejemplo anterior se muestra a definición de la clase Animal Métodos:
Los métodos son funciones definidas dentro de una clase que operan sobre los atributos de la instancia. Se definen como cualquier otra función, pero su primer parámetro es siempre self, que representa la instancia.
Figura 46
Primer parámetro Self
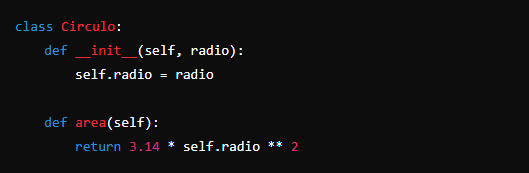
Definición del primer parámetro Self Atributos y métodos de clase:
Los atributos de clase son variables que pertenecen a la clase y son compartidos por todas las instancias. Se definen fuera de cualquier método.
Figura 47
Atributos en clases
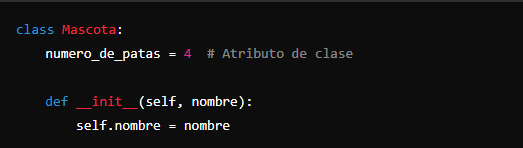
Ejemplo de atributo de clase mascota “4” Herencia
La herencia permite crear una nueva clase basada en una clase existente. La nueva clase (subclase) hereda atributos y métodos de la clase base (superclase).
Figura 48
Ejemplo de herencia en clases
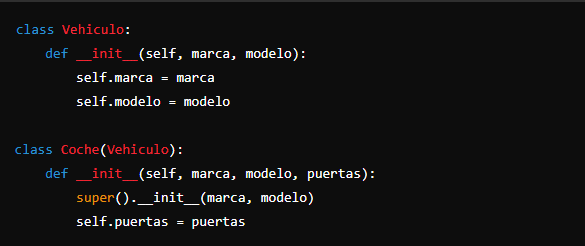
Gráfica de dos clases que mantienen una herencia en común Encapsulamiento
El es el principio de ocultar los detalles internos de la implementación de una clase. En Python, los atributos y métodos privados se denotan con un guion bajo _.
Figura 49
Encapsulamiento
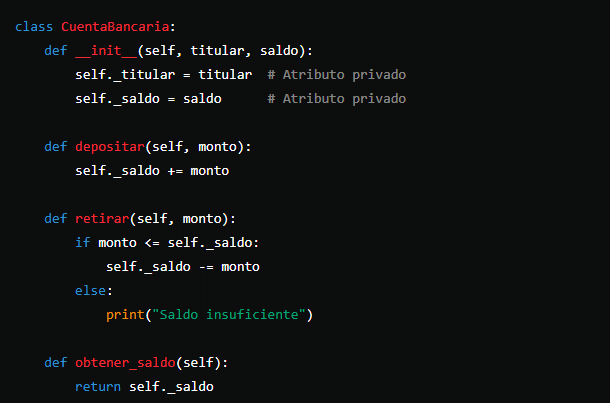
Ejemplo de encapsulamiento en Python Polimorfismo
El polimorfismo permite que diferentes clases utilicen la misma interfaz. En Python, esto se puede lograr mediante la herencia y la sobreescritura de métodos.
Figura 50
Ejemplo de
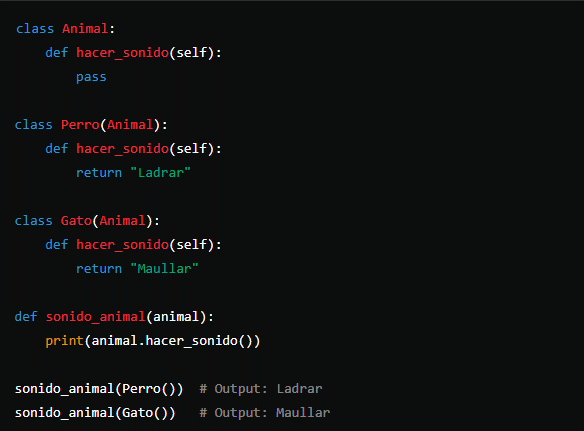
Ejemplo interfaz clase animal Encapsulamiento
Es un principio de la programación orientada a objetos que restringe el acceso directo a algunos de los componentes de un objeto. Los atributos y métodos privados se ocultan y solo se pueden acceder a través de métodos públicos definidos en la clase. Esto mejora la modularidad y protege la integridad de los datos.
Interfaz Compartida
Es un conjunto de métodos que diferentes clases pueden implementar, lo que permite que los objetos de estas clases sean tratados de manera uniforme. En la programación orientada a objetos, una interfaz define un contrato que las clases deben cumplir, asegurando que los métodos especificados en la interfaz estén presentes en las clases que la implementan.
-
-
-
Introducción
P
ython permite la creación de programas simples y eficientes para una amplia variedad de aplicaciones. Su sintaxis clara y legible, junto con una vasta colección de bibliotecas y recursos, hace que sea particularmente fácil de aprender y utilizar para resolver problemas cotidianos y desarrollar soluciones rápidamente.
-
12.1 Programas simples en Python12.2 Aplicaciones de funciones a modelo matemático de negocios y visualización: costo, lucro y ganancia.Una de las principales razones por las que Python es sencillo de aprender es su diseño intuitivo. A diferencia de otros lenguajes de programación que pueden tener una sintaxis más compleja, Python se asemeja al lenguaje humano, lo que facilita su comprensión y escritura.
Además, la comunidad de Python es extensa y activa, proporcionando numerosos tutoriales, documentación y foros de soporte que ayudan a los nuevos programadores a resolver problemas y aprender nuevas habilidades.
Ejemplo 1: Hola MundoEl programa más básico y una excelente manera de comenzar con Python es el clásico "Hola Mundo". Este programa imprime un mensaje simple en la pantalla.
Figura 51
Código para “Hola, Mundo”
Ejemplo 2: Calculadora Sencilla
La función print() se utiliza para mostrar el texto "Hola, Mundo!" en la consola. Una calculadora básica que realiza operaciones aritméticas simples como suma, resta, multiplicación y división.
Figura 52
Código para operaciones aritméticas simples
Ejemplo 3: Conversión de Temperatura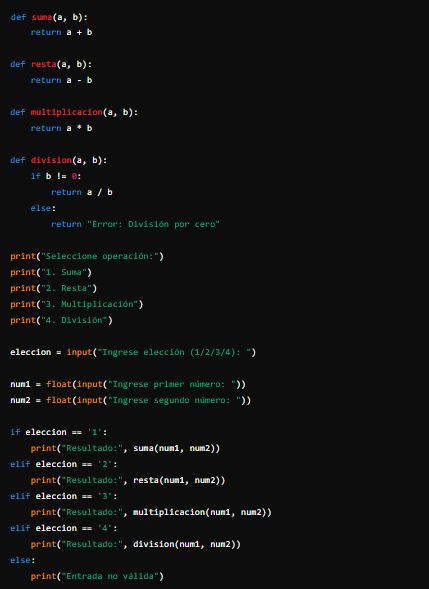
Este programa define cuatro funciones para realizar las operaciones aritméticas. Luego, solicita al usuario que seleccione una operación y que ingrese dos números. Finalmente, realiza la operación seleccionada y muestra el resultado. Un programa que convierte temperaturas de grados Celsius a grados Fahrenheit.
Figura 53
Código para convertir temperaturas
Ejemplo 4: Generador de Contraseñas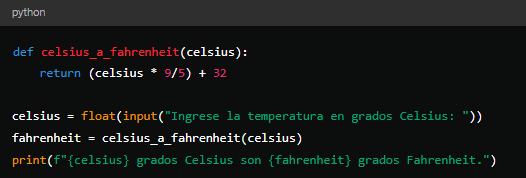
Este programa define una función celsius_a_fahrenheit() que convierte una temperatura dada en grados Celsius a grados Fahrenheit. Solicita al usuario que ingrese una temperatura en grados Celsius y muestra la temperatura convertida. Un programa simple que genera una contraseña aleatoria de una longitud especificada por el usuario.
Figura 54
Código para generar una contraseña
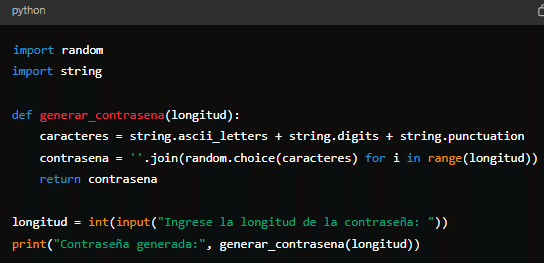
Este programa utiliza las bibliotecas random y string para generar una contraseña aleatoria. La función generar_contrasena() crea una cadena de caracteres aleatorios de la longitud especificada por el usuario y la muestra en pantalla. Para practicar lo aprendido, intenta crear un programa que calcule el índice de masa corporal (IMC) de una persona. El IMC se calcula dividiendo el peso en kilogramos entre la altura en metros al cuadrado.
En esta sección, vamos a unir lo que hemos visto en matemáticas teóricas, especialmente las funciones aplicadas a los negocios, con las herramientas del cálculo diferencial e integral y los límites. Utilizaremos Python para modelar un negocio y veremos conceptos clave como el costo promedio, utilizando asíntotas y límites.
Vamos a utilizar Google Colab para llevar a cabo nuestras actividades. Google Colab nos permite escribir y ejecutar código Python directamente en el navegador, lo cual es muy útil para este tipo de ejercicios.
Asíntotas y límites
Una asíntota es una línea a la que una función se aproxima, pero nunca toca. Este concepto está íntimamente relacionado con los límites en matemáticas.
Ejemplo de Asíntotas con PythonFigura 55
Importación de las librerías necesarias

Figura 1: Prueba de Imagen Figura 56
Definición de la función f(x) y visualización de asíntotas
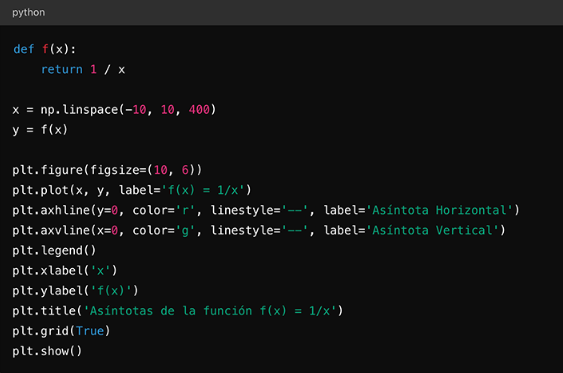
Figura 1: Prueba de Imagen En este ejemplo, podemos observar dos tipos de asíntotas:
- Asíntota vertical: A medida que x tiende a cero, f(x) tiende a infinito.
- Asíntota horizontal: A medida que x tiende a infinito, f(x) tiende a cero.
Cálculo del costo promedio
Ahora veremos cómo aplicar el concepto de límites para calcular el costo promedio en un negocio.
Definición del costo promedio:
El costo promedio es el costo total dividido por el número de ítems producidos. Si el costo total C(x) está dado por una parte fija y una parte variable, el costo promedio C̄ se define como:
Cˉ=C(x)xCˉ=xC(x)
Ejemplo de costo promedio con Python:
Definimos el costo total C(x) y calculamos el costo promedio:
Figura 57
Cálculo del costo promedio
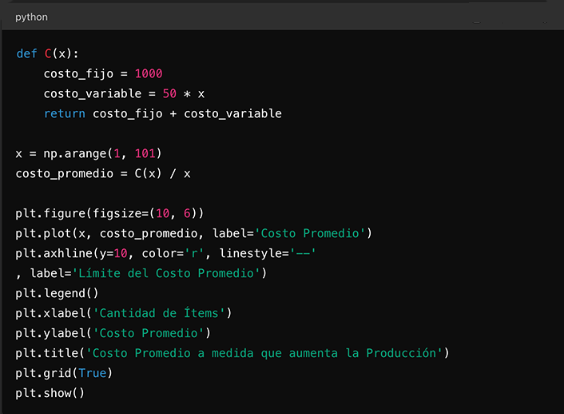
En este gráfico, se puede observar cómo el costo promedio disminuye a medida que aumenta la cantidad de ítems producidos. El costo promedio tiende a estabilizarse alrededor de un valor límite a medida que la producción crece.
-
-
-
Introducción
P
ython ha ganado gran popularidad debido a su facilidad de uso y su capacidad para escalar hacia aplicaciones más complejas. Desde simples scripts de automatización hasta sistemas de aprendizaje automático y aplicaciones web de gran escala, Python proporciona las herramientas necesarias para abordar una amplia gama de problemas. Su ecosistema, rico en bibliotecas como NumPy, Pandas, TensorFlow, Flask y Django, permite a los desarrolladores implementar soluciones avanzadas de manera eficiente. La comunidad activa de Python también asegura la constante mejora del lenguaje y sus herramientas, proporcionando soporte y recursos valiosos para el aprendizaje continuo y la resolución de problemas.
-
13. Programas más avanzados en Python13.1 Herramientas de cálculo con Python para modelaje de funciones aplicado a negocios: análisis marginal
A continuación, se presentan ejemplos de programas avanzados en Python en diversas áreas, ilustrando cómo este lenguaje puede utilizarse para resolver problemas complejos.
Ejemplo 1. Análisis de Datos con Pandas
Figura 57:
Este programa carga un conjunto de datos, realiza limpieza de datos, convierte una columna a formato de fecha, genera un resumen estadístico y agrupa las ventas por año. Ejemplo 2. Desarrollo Web con Flask
Figura 58
Este programa utiliza Flask para crear una aplicación web simple con una ruta de inicio y una ruta que procesa un formulario para saludar al usuario por su nombre. Ejemplo 3. Aprendizaje Automático con Scikit-Learn
Figura 59
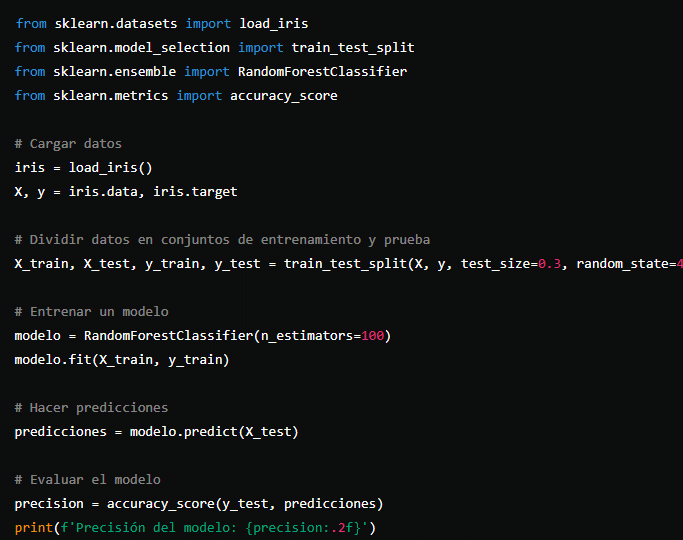
Este programa carga el conjunto de datos de iris, divide los datos en conjuntos de entrenamiento y prueba, entrena un modelo de bosque aleatorio y evalúa su precisión. 13.2 Herramientas de cálculo con Python para modelaje de funciones aplicado a negocios: oferta y demanda y producción totalEn esta sección, exploraremos cómo utilizar Python para analizar puntos críticos en funciones matemáticas aplicadas a los negocios. Nos centraremos en la identificación de máximos y mínimos relativos, así como en cómo estos conceptos se aplican en el análisis marginal de funciones de costo, ingreso y lucro. Estos conocimientos son esenciales para tomar decisiones estratégicas en un negocio.
Puntos críticos y máximos/mínimos relativos
Un punto crítico de una función se encuentra cuando su primera derivada respecto a x se iguala a cero. Matemáticamente, esto se expresa como: f′(x)=0.
El valor de x que satisface esta ecuación es el punto crítico. Este punto puede ser un máximo, un mínimo o un punto de inflexión.
Análisis de máximos y mínimos relativos
Criterio de la primera derivada: Para determinar si un punto crítico es un máximo o un , analizamos el signo de la primera derivada en intervalos cercanos a ese punto:
Si f′(x) es positiva en un intervalo y negativa en otro, el punto crítico es un .
Si f′(x) es negativa en un intervalo y positiva en otro, el punto crítico es un mínimo relativo.
Criterio de la segunda derivada: El criterio de la segunda derivada proporciona un método más directo para clasificar puntos críticos:
Si la segunda derivada f′′(x) evaluada en el punto crítico es menor que cero, el punto es un máximo relativo.
Si f′′(x) evaluada en el punto crítico es mayor que cero, el punto es un mínimo relativo.
Aplicación en negocios: análisis marginal
El análisis marginal se refiere a la evaluación de la tasa de cambio instantánea en funciones de negocio, tales como el costo, el ingreso y el lucro.
Funciones marginales
Costo marginal: El costo marginal se define como la derivada de la función de costo total C(x): C′(x). Representa la tasa instantánea de cambio del costo total con respecto al número de productos producidos.
Ingreso marginal: El ingreso marginal es la derivada de la función de ingreso total R(x): R′(x). Indica la tasa instantánea de cambio del ingreso total por cada unidad adicional vendida.
Lucro marginal: El lucro marginal es la derivada de la función de lucro total P(x), que es la diferencia entre ingreso y costo: P′(x)=R′(x)−C′(x)
Problema: Una compañía produce tanques de gasolina para autos. El costo total de producir x tanques está dado por la función C(x). Queremos encontrar el costo marginal y el costo exacto de producir un tanque adicional en un nivel de producción de 500 tanques por semana.
Solución: Definimos la función de costo total C(x) y calculamos su derivada.
Figura 60

Evaluamos el costo marginal en x=500:
Figura 61

Calculamos el costo exacto de producir el tanque 501:
Figura 62
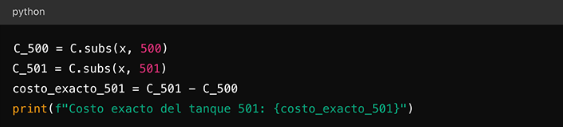
En esta sección, vamos a aplicar la teoría aprendida sobre costos, ingresos y lucros marginales utilizando Python. Esto nos permitirá visualizar de manera práctica cómo se comportan estas funciones en un entorno de negocios. ¡Vamos a preparar nuestro entorno y comenzar con los cálculos!
Preparación del entorno
Primero, necesitamos preparar nuestro entorno de trabajo en Python. Definiremos nuestras funciones de costo y precio para luego calcular el ingreso y el lucro.
Definición de funciones
C(x)=50+20x
P(x)=100−2x
Figura 63
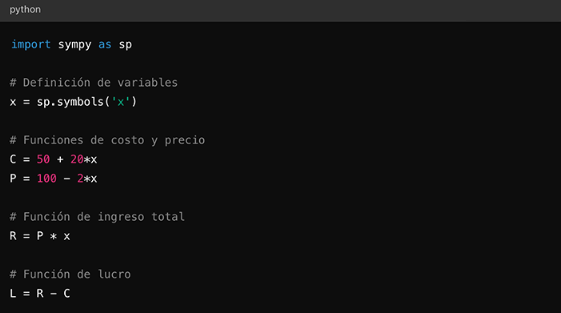
Derivadas y funciones marginales
C′(x)=d/dx(50+20x)
R′(x)=d/dx(P(x)⋅x)
L′(x)=d/dx(R(x)−C(x))
Figura 64

Visualización
Para comprender mejor cómo se comportan estas funciones, vamos a visualizar los resultados en gráficos. Supongamos que estamos produciendo entre 0 y 40 unidades. Calcularemos y graficaremos el costo, el ingreso y el lucro total, así como sus derivadas marginales.
Figura 65
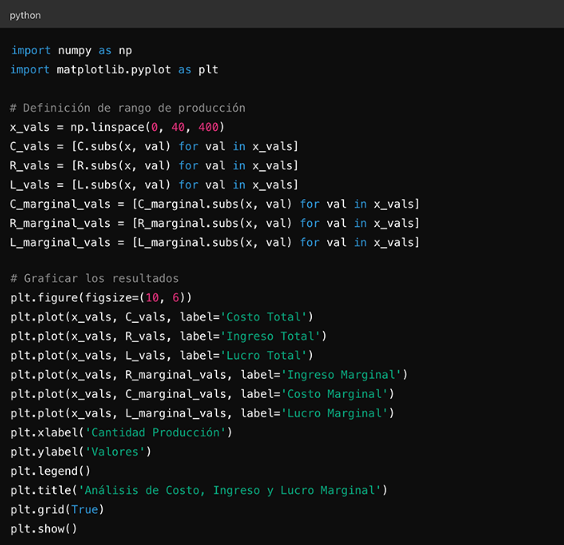
Interpretación de resultados Al visualizar los resultados, podemos observar lo siguiente:
- Costo total: Incrementa linealmente con la cantidad producida debido al término 20x.
- Ingreso total: Inicialmente incrementa, pero luego decrece debido a la función de demanda P(x).
- Lucro total: Es la diferencia entre el ingreso y el costo. Se observa el punto máximo de lucro.
- Ingreso marginal: Muestra cómo cambia el ingreso total con cada unidad adicional vendida.
- Costo marginal: Muestra cómo cambia el costo total con cada unidad adicional producida.
- Lucro marginal: Indica la rentabilidad de producir una unidad adicional.
Máximo relativo
Es el punto en una función donde el valor de la función es mayor que en los puntos inmediatamente adyacentes. También conocido como máximo local, es un punto x=c tal que f(c)≥f(x) para todos los x cercanos a c.
Mínimo relativo
Es el punto en una función donde el valor de la función es menor que en los puntos inmediatamente adyacentes. También conocido como mínimo local, es un punto x=c tal que f(c)≤f(x) para todos los x cercanos a c.
-
-
-
Introducción
P
ython es un lenguaje de programación versátil utilizado en una amplia variedad de disciplinas, que van desde el desarrollo web hasta el análisis de datos y el aprendizaje automático.
Para escribir y ejecutar código Python, existen varias herramientas populares, entre las que se incluyen Visual Studio Code (VS Code), Jupyter Labs y Google Colab. Cada una de estas herramientas tiene características únicas que las hacen adecuadas para diferentes contextos de uso.
-
14.1 Visual Studio Code (VS Code)14.2 Jupyter labs
es un editor de código fuente gratuito y de código abierto desarrollado por Microsoft. Es muy popular entre los desarrolladores debido a su flexibilidad, personalización y extensibilidad. Entre sus características principales se incluyen:
Extensiones: VS Code admite una amplia variedad de extensiones que mejoran su funcionalidad, como soporte para Python, depuración, control de versiones, entre otras.
Depuración integrada: Ofrece herramientas de depuración avanzadas que facilitan la identificación y corrección de errores en el código.
Terminal integrada: Permite ejecutar comandos directamente desde el editor, lo que resulta útil para instalar paquetes o ejecutar scripts.
IntelliSense: Proporciona autocompletado y sugerencias de código basadas en el análisis del código, lo que mejora la productividad (López & Martínez, 2019).
14.3 Google ColabJupyter Labs es una evolución de los populares y proporciona un entorno interactivo para el desarrollo de código en Python, especialmente útil para el análisis de datos, la visualización y el aprendizaje automático.
Figura 66
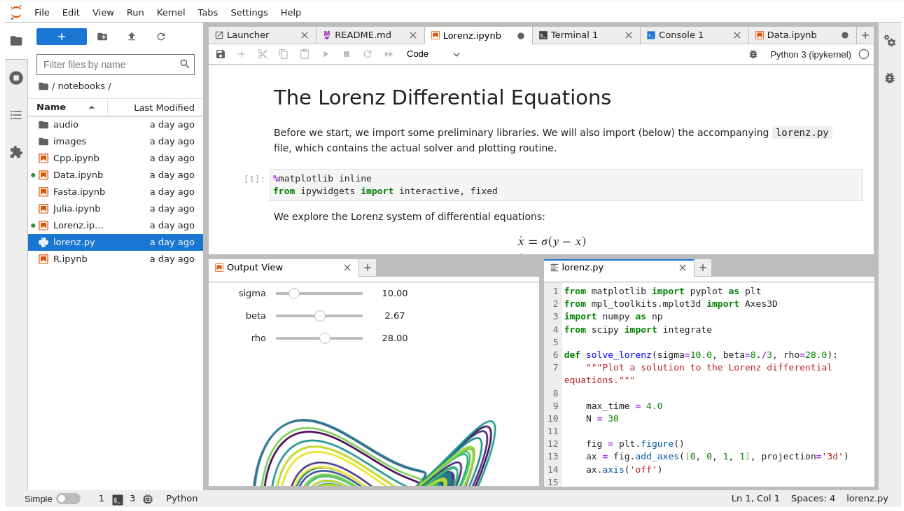
Entre las características principales se incluyen:
Celdas interactivas: Permiten la escritura y ejecución de código en fragmentos llamados celdas, que pueden contener código, texto, visualizaciones, entre otros.
Visualización de datos: Integra bibliotecas como Matplotlib, Seaborn y Plotly para la creación de gráficos y visualizaciones interactivas.
Entorno multilingüe: Aunque es especialmente conocido por su soporte para Python, Jupyter Labs también puede ser utilizado con otros lenguajes como R y Julia.
Documentación y notas: Permite incluir texto y ecuaciones en lenguaje Markdown, lo que es útil para documentar el código y los resultados (Gómez & Torres, 2020).
14.4 Elaboración y planeación de modelo simple de negocio usando herramientas de cálculo con PythonGoogle Colab es una plataforma en la nube basada en Jupyter Notebooks que permite a los usuarios escribir y ejecutar código Python directamente en su navegador. Entre las características principales se incluyen:
Acceso gratuito a recursos de cómputo: Google Colab proporciona acceso gratuito a GPUs y TPUs, lo que es especialmente útil para tareas de aprendizaje profundo y computación intensiva.
Colaboración: Permite la colaboración en tiempo real, similar a Google Docs, donde múltiples usuarios pueden trabajar en el mismo cuaderno.
Integración con Google Drive: Facilita el almacenamiento y acceso a archivos, permitiendo guardar y cargar datos directamente desde Google Drive.
Preinstalación de bibliotecas: Viene con muchas bibliotecas de Python preinstaladas, lo que simplifica el entorno de desarrollo (Pérez & López, 2021).
Tabla 1
Comparación y uso
Herramienta Uso VS Code Ideal para el desarrollo de aplicaciones completas y proyectos donde se requiere un entorno de desarrollo integrado (IDE) robusto. Jupyter Labs Perfecto para investigación, análisis de datos y educación, proporcionando una experiencia interactiva. Google Colab Excelente para el trabajo colaborativo en proyectos de ciencia de datos y aprendizaje automático, especialmente cuando se necesita acceso a hardware potente. Tabla: Comparación de Herramientas y sus Usos VS CodeIdeal para el desarrollo de aplicaciones completas y proyectos donde se requiere un entorno de desarrollo integrado (IDE) robusto.Jupyter LabsPerfecto para investigación, análisis de datos y educación, proporcionando una experiencia interactiva.Google ColabExcelente para el trabajo colaborativo en proyectos de ciencia de datos y aprendizaje automático, especialmente cuando se necesita acceso a hardware potente.Fuente: Pérez & López, 2021
Python, con su robusto ecosistema de bibliotecas y herramientas de cálculo, facilita este proceso a través de la automatización de cálculos, la simulación de escenarios y la visualización de datos.
Un modelo de negocio describe cómo una empresa crea, entrega y captura valor. En su forma más simple, un modelo de negocio incluye los ingresos, costos y beneficios. Los elementos clave incluyen:
Estructura de costos: Los costos fijos y variables relacionados con la producción y la operación.
Fuentes de ingresos: Los métodos por los cuales la empresa genera ingresos, como ventas de productos, servicios, suscripciones, etc.
Propuesta de valor: El valor que la empresa ofrece a sus clientes.
Python ofrece varias bibliotecas que facilitan el desarrollo de modelos de negocio:
NumPy y SciPy: Estas bibliotecas son esenciales para realizar cálculos numéricos eficientes, como la optimización de costos y el análisis de sensibilidad.
Pandas: Ideal para la manipulación y análisis de datos. Permite la organización de datos en estructuras tabulares (DataFrames) y facilita operaciones como la agregación, filtrado y análisis de series temporales (López & Gómez, 2019).
Matplotlib y Seaborn: Utilizadas para la visualización de datos. Ayudan a crear gráficos y diagramas que pueden ilustrar tendencias de ventas, costos y otras métricas clave (Martínez & Torres, 2020).
14.1.1 Pasos para la elaboración del modelo
Recopilación de Datos: Recopilar datos históricos de ventas, costos y otras variables relevantes. Esto puede incluir datos de mercado, competencia y comportamiento del consumidor.
Análisis de Datos: Utilizar Pandas para limpiar y analizar los datos, identificar patrones y calcular métricas clave como costos unitarios, ingresos medios y márgenes de beneficio.
Modelado Financiero:
Proyección de Ingresos: Usar técnicas de análisis de series temporales o regresión para proyectar ingresos futuros basados en datos históricos y supuestos de crecimiento.
Estimación de Costos: Modelar costos fijos y variables, y proyectar cómo estos cambian con diferentes niveles de producción.
Cálculo de Beneficios: Restar los costos proyectados de los ingresos proyectados para calcular los beneficios netos.
Simulación de Escenarios: Utilizar SciPy para realizar análisis de sensibilidad y simulaciones de Monte Carlo, lo que permite evaluar cómo diferentes variables afectan el desempeño financiero del negocio.
Visualización y Presentación: Utilizar Matplotlib y Seaborn para crear gráficos que visualicen las proyecciones financieras, escenarios y métricas clave, facilitando la presentación de resultados a stakeholders.
Por ejemplo, una startup que planea lanzar un nuevo producto puede usar estas herramientas para proyectar ingresos basados en diferentes estrategias de precios y niveles de producción, evaluar los costos relacionados y analizar el impacto de diferentes escenarios de mercado en el beneficio neto (Pérez & Sánchez, 2021).
Jupyter Notebooks
Es un entorno interactivo basado en la web que permite a los usuarios crear y compartir documentos que contienen código en vivo, ecuaciones, visualizaciones y texto narrativo. Es ampliamente utilizado en análisis de datos, visualización y desarrollo de prototipos de código.
Visual Studio Code
Es un editor de código fuente desarrollado por Microsoft, altamente extensible y que soporta una amplia variedad de lenguajes de programación. Es conocido por su interfaz intuitiva, integración con Git y un robusto ecosistema de extensiones que facilitan el desarrollo de software en múltiples plataformas.
-
-
-
Introducción
J
upyter Notebook y Google Colab son entornos interactivos ampliamente utilizados para el desarrollo de modelos en Python. Estos entornos son especialmente útiles en áreas como la ciencia de datos, el aprendizaje automático, la visualización de datos y el análisis exploratorio, ya que permiten combinar código, texto explicativo, ecuaciones matemáticas y visualizaciones en un solo documento interactivo.
-
15.1 Jupyter Notebook15.2 Google Colab
Jupyter Notebook es una aplicación web que permite crear y compartir documentos que contienen en vivo, ecuaciones, visualizaciones y texto narrativo. Es especialmente popular en la comunidad de ciencia de datos debido a su capacidad para facilitar un flujo de trabajo interactivo.
Entre sus características principales se encuentran:
Celdas de código y texto: Permiten la ejecución de fragmentos de código Python y la inclusión de texto explicativo, lo que es ideal para documentar el proceso de análisis y los resultados obtenidos.
Soporte multilenguaje: Aunque es más conocido por su uso con Python, Jupyter también admite otros lenguajes de programación a través de diferentes "kernels".
Visualización de datos: Integra fácilmente de visualización como Matplotlib, Seaborn y Plotly, entre otras, para crear gráficos y visualizaciones interactivas (Gómez & Torres, 2019).
15.3 Pasos para la elaboración de un modeloGoogle Colab es una plataforma gratuita basada en Jupyter Notebooks, pero con la ventaja añadida de estar en la nube. Esto permite a los usuarios acceder y ejecutar su código desde cualquier lugar sin necesidad de configuraciones locales complejas. Entre sus características principales se encuentran:
Acceso a hardware potente: Ofrece acceso gratuito a GPUs y TPUs, lo cual es beneficioso para tareas que requieren altos recursos computacionales, como el entrenamiento de modelos de aprendizaje profundo.
Colaboración en tiempo real: Permite a varios usuarios colaborar en el mismo notebook de manera simultánea, facilitando el trabajo en equipo y la enseñanza.
Integración con Google Drive: Facilita el almacenamiento y la compartición de notebooks y datos, simplificando el manejo de archivos (Pérez & López, 2020).
15.4. Modelo matemático de negocio con análisis marginal y producción total completo con Python.Importación de bibliotecas y datos:
El proyecto comienza importando las bibliotecas necesarias, como NumPy, Pandas, Matplotlib, Seaborn, entre otras.
Se carga el conjunto de datos desde una fuente local o en línea.
Exploración y preprocesamiento de datos:
Se realiza un análisis exploratorio de datos (EDA) para comprender la estructura y las características del conjunto de datos.
Se limpian los datos, manejando valores nulos, duplicados y transformando variables si es necesario.
Desarrollo del modelo:
Se selecciona y entrena un modelo utilizando algoritmos de aprendizaje automático disponibles en bibliotecas como Scikit-learn o TensorFlow.
Se ajustan los hiperparámetros y se validan los resultados del modelo usando técnicas como la validación cruzada.
Evaluación y visualización de resultados:
Se evalúan las métricas de rendimiento del modelo, como precisión, recall, F1-score, entre otras.
Se crean visualizaciones para interpretar los resultados y los patrones identificados.
Documentación y presentación:
Se documenta cada paso del proceso en celdas de texto, proporcionando contexto y explicaciones detalladas.
Se generan informes y gráficos que facilitan la comunicación de los hallazgos a los stakeholders o colaboradores.
Por ejemplo, un analista de datos puede usar Jupyter Notebook o Google Colab para desarrollar un modelo de predicción de ventas, explorando datos históricos, entrenando un modelo de regresión y visualizando las proyecciones futuras de ventas en diferentes escenarios (Martínez & Sánchez, 2021).
El modelo matemático de negocio es una herramienta crucial para entender y optimizar el funcionamiento de una empresa. Este modelo puede incluir componentes como el análisis marginal y la producción total, utilizando Python para realizar cálculos precisos y visualizaciones detalladas.
El análisis marginal se centra en cómo cambian los costos y beneficios con respecto a pequeñas variaciones en el nivel de producción o ventas. Es fundamental para la toma de decisiones empresariales, ya que ayuda a determinar el punto óptimo de producción o fijación de precios.
Costo marginal (CM): Es el costo adicional incurrido al producir una unidad adicional de un producto. Matemáticamente, se define como la derivada del costo total con respecto a la cantidad producida, es decir:
donde C(q) es la función de costo total y q es la cantidad producida.
Ingreso marginal (IM): Es el ingreso adicional obtenido al vender una unidad adicional. Se calcula como la derivada del ingreso total respecto a la cantidad vendida:
donde R(q) es la función de ingreso total (Pérez & Martínez, 2019).
La producción total se refiere a la cantidad total de bienes producidos por una empresa en un periodo determinado. Es crucial para evaluar la eficiencia y capacidad de producción de una empresa.
Función de producción: Describe la relación entre los insumos utilizados (trabajo, capital, etc.) y la cantidad de producción generada. Puede expresarse como: Q=f(L,K), donde Q es la producción total, L representa el trabajo y K el capital. Esta función ayuda a determinar cómo los cambios en los insumos afectan la producción total (Gómez & Torres, 2020).
Python, con sus bibliotecas como NumPy, Pandas y Matplotlib, permite la implementación eficiente de modelos matemáticos de negocios. A continuación, se describe un flujo de trabajo típico:
Definición de funciones de costo e ingreso:
Se definen las funciones de costo total C(q) e ingreso total R(q) en términos de la cantidad q. Estas funciones pueden incluir componentes fijos y variables.
Cálculo de derivadas:
Se utilizan herramientas como SymPy para calcular simbólicamente las derivadas, obteniendo así las funciones de costo marginal e ingreso marginal.
Optimización de beneficios:
Se determina el nivel de producción q que maximiza el beneficio, encontrado cuando IM = CM. Esto se puede hacer utilizando métodos numéricos o de optimización, como scipy.optimize.
Visualización de resultados:
Se utilizan bibliotecas de visualización como Matplotlib para graficar las funciones de costo, ingreso, beneficio y sus respectivas derivadas. Esto facilita la interpretación de los resultados y la toma de decisiones.
Este modelo puede ser aplicado, por ejemplo, en una empresa manufacturera que busca optimizar su producción para maximizar el beneficio. El análisis marginal ayudará a determinar cuántas unidades adicionales deben producirse o no para lograr la máxima rentabilidad (López & Sánchez, 2021).
Bibliotecas
Conjunto de módulos y funciones predefinidos que pueden ser reutilizados en diferentes programas para realizar tareas específicas. En programación, las bibliotecas permiten simplificar el desarrollo al ofrecer herramientas ya creadas para manejar desde cálculos matemáticos hasta interfaces de usuario.
Código
Conjunto de instrucciones escritas en un lenguaje de programación que una computadora puede interpretar y ejecutar para realizar una tarea específica. El código puede variar desde simples secuencias de comandos hasta complejos sistemas de software.
-
-
Reto 4. Presentación final del proyecto basado en Cálculo aplicado en Finanzas o Negocios con Python
-
-
Abrir
Tema
Pensamiento computacional
Instrucciones
Trabajo autónomo del estudiante
Vamos a usar el portal CODE.ORG para profundizar tu conocimiento en pensamiento computacional.
-
Regístrate en www.code.org con tu correo electrónico de Gmail.
-
Crea una contraseña para este sitio.
-
Inicia sesión.
-
Únete al curso de Pensamiento Computacional con el siguiente código: (Permitir que el docente semestre a semestre pueda escribir el código)
Novena semana de clases:
Se habilita la Unidad: Introducción al diseño de aplicaciones
Décima semana de clases:
Prueba de la Unidad: Introducción al diseño de aplicaciones
Décimo primera semana de clases:
Se habilita la Unidad: Variables, Condicionales y Funciones
Décimo segunda semana de clases:
Prueba de la Unidad: Variables, Condicionales y Funciones
Décimo tercera semana de clases:
Se habilita la Unidad: Listas, Bucles y Recorridos
Décimo cuarta semana de clases:
Prueba de la Unidad: Listas, Bucles y Recorridos
Décimo quinta semana de clases:
Se habilita: Encuesta de fin de curso
Décimo sexta semana de clases:
No hay actividades en Code.org
- Tomado de Learn computer science. Change the world. (n.d.). Code.org. https://www.code.org/
-
-
-
-
RDA2 - Ruta de Aprendizaje Tarea
- Instrucciones en el pdf adjunto.
- Entregar hasta el domingo 17 de agosto. 23h59.
- Trabajo individual
- Para personas que obtuvieron D (menos de 30) en el RDA2 y el resto de RDAs mayor o igual a 30.
No disponible hasta que: se pertenezca al grupo Ruta RDA 2
-
-
-
RDA3 - Ruta de Aprendizaje Tarea
- Instrucciones en el pdf adjunto.
- Entregar hasta el doming 17 de agosto. 23h59.
- Trabajo individual
- Para personas que obtuvieron D en el RDA3 ( menos de 30 ) y en el resto de RDAs mayor o igual a 30.
No disponible hasta que: se pertenezca al grupo Ruta RDA 3
-
-
-
- Blanco, F., & García, J. (2019). Cálculo diferencial e integral. Editorial Matemáticas Avanzadas.
- Gómez, A., & Rodríguez, M. (2019). Análisis de costos y rentabilidad en empresas. Editorial Económica.
- López, S., & Torres, R. (2020). Fundamentos de álgebra y funciones. Editorial Académica.
- Martínez, C., & Pérez, L. (2018). Matemáticas aplicadas a las ciencias e ingenierías. Editorial Técnica.
- Martínez, J., & López, S. (2020). Estrategias de precios en mercados competitivos. Editorial Mercados.
- Torres, E., & Castillo, R. (2021). Fundamentos de la administración financiera. Editorial Gestión Empresarial.
-
- Gómez, M., & Sánchez, D. (2020). Aplicaciones del cálculo: Ciencia e ingeniería. Editorial Técnica.
- López, J., & Pérez, A. (2019). Cálculo diferencial e integral en una variable. Editorial Académica.
- Torres, E., & Castillo, R. (2021). Fundamentos de la matemática avanzada. Editorial Científica.
-
- Gómez, M., & Torres, A. (2020). Jupyter y Python para análisis de datos. Editorial Informática.
- López, J., & Martínez, S. (2019). Herramientas de desarrollo para Python: una guía práctica. Editorial Técnica.
- Pérez, L., & López, J. (2021). Ciencia de datos en la nube con Google Colab. Editorial Académica.
-
- Gómez, M., & López, J. (2019). Cálculo diferencial e integral aplicado a la economía. Editorial Académica.
- Martínez, S., & Torres, A. (2020). Visualización de datos y análisis económico con Python. Editorial Técnica.
- Pérez, L., & Sánchez, R. (2021). Modelos matemáticos en la gestión empresarial. Editorial Universitaria.
-
- Gómez, M., & López, J. (2019). Cálculo diferencial e integral: Aplicaciones y conceptos clave. Editorial Académica.
- Martínez, S., & Torres, A. (2020). Visualización y análisis de funciones matemáticas con Python. Editorial Técnica.
- Pérez, L., & Sánchez, R. (2021). Aplicaciones del cálculo en las ciencias económicas y naturales. Editorial Universitaria.
-
- Gómez, M., & Rodríguez, J. (2019). GeoGebra y su aplicación en la enseñanza de las matemáticas. Editorial Educativa.
- Martínez, S., & Torres, A. (2020). Simulación y modelado en ingeniería: Herramientas y aplicaciones. Editorial Técnica.
- Pérez, L., & López, J. (2021). Tecnologías educativas: Integración de software en la enseñanza de las ciencias. Editorial Académica.
-
- Gómez, M., & Rodríguez, J. (2019). GeoGebra y su aplicación en la enseñanza de las matemáticas. Editorial Educativa.
- Martínez, S., & Torres, A. (2020). Simulación y modelado en ingeniería: Herramientas y aplicaciones. Editorial Técnica.
- Pérez, L., & López, J. (2021). Tecnologías educativas: Integración de software en la enseñanza de las ciencias. Editorial Académica.
-
- Gómez, M., & Rodríguez, J. (2019). GeoGebra y su aplicación en la enseñanza de las matemáticas. Editorial Educativa.
- Martínez, S., & Torres, A. (2020). Simulación y modelado en ingeniería: Herramientas y aplicaciones. Editorial Técnica.
- Pérez, L., & López, J. (2021). Tecnologías educativas: Integración de software en la enseñanza de las ciencias. Editorial Académica.
-
- Gómez, M., & Rodríguez, J. (2019). GeoGebra y su aplicación en la enseñanza de las matemáticas. Editorial Educativa.
- Martínez, S., & Torres, A. (2020). Simulación y modelado en ingeniería: herramientas y aplicaciones. Editorial Técnica.
- Pérez, L., & López, J. (2021). Tecnologías educativas: integración de software en la enseñanza de las ciencias. Editorial Académica.
-
- Gómez, M., & Rodríguez, J. (2019). GeoGebra y su aplicación en la enseñanza de las matemáticas. Editorial Educativa.
- Martínez, S., & Torres, A. (2020). Simulación y modelado en ingeniería: Herramientas y aplicaciones. Editorial Técnica.
- Pérez, L., & López, J. (2021). Tecnologías educativas: integración de software en la enseñanza de las ciencias. Editorial Académica.
-
- Gómez, M., & Rodríguez, J. (2019). GeoGebra y su aplicación en la enseñanza de las matemáticas. Editorial Educativa.
- Martínez, S., & Torres, A. (2020). Simulación y modelado en ingeniería: Herramientas y aplicaciones. Editorial Técnica.
- Pérez, L., & López, J. (2021). Tecnologías educativas: Integración de software en la enseñanza de las ciencias. Editorial Académica.
-
- Gómez, M., & Rodríguez, J. (2019). GeoGebra y su aplicación en la enseñanza de las matemáticas. Editorial Educativa.
- Martínez, S., & Torres, A. (2020). Simulación y modelado en ingeniería: Herramientas y aplicaciones. Editorial Técnica.
- Pérez, L., & López, J. (2021). Tecnologías educativas: Integración de software en la enseñanza de las ciencias. Editorial Académica.
-
- Gómez, M., & Rodríguez, J. (2019). GeoGebra y su aplicación en la enseñanza de las matemáticas. Editorial Educativa.
- Martínez, S., & Torres, A. (2020). Simulación y modelado en ingeniería: herramientas y aplicaciones. Editorial Técnica.
- Pérez, L., & López, J. (2021). Tecnologías educativas: integración de software en la enseñanza de las ciencias. Editorial Académica.
-
- Gómez, M., & Rodríguez, J. (2019). GeoGebra y su aplicación en la enseñanza de las matemáticas. Editorial Educativa.
- Martínez, S., & Torres, A. (2020). Simulación y modelado en ingeniería: Herramientas y aplicaciones. Editorial Técnica.
- Pérez, L., & López, J. (2021). Tecnologías educativas: Integración de software en la enseñanza de las ciencias. Editorial Académica.
-
- Gómez, M., & Rodríguez, J. (2019). GeoGebra y su aplicación en la enseñanza de las matemáticas. Editorial Educativa.
- Martínez, S., & Torres, A. (2020). Simulación y modelado en ingeniería: Herramientas y aplicaciones. Editorial Técnica.
- Pérez, L., & López, J. (2021). Tecnologías educativas: Integración de software en la enseñanza de las ciencias. Editorial Académica.
-
-
-
-
Descargar el contenido de la Clase 1
Descargar el contenido de la Clase 2
Descargar el contenido de la Clase 3
Descargar el contenido de la Clase 4
Descargar el contenido de la Clase 5
Descargar el contenido de la Clase 6
Descargar el contenido de la Clase 7
Descargar el contenido de la Clase 8
Descargar el contenido de la Clase 9
Descargar el contenido de la Clase 10
Descargar el contenido de la Clase 11
Descargar el contenido de la Clase 12
Descargar el contenido de la Clase 13
Descargar el contenido de la Clase 14
Descargar el contenido de la Clase 15
Descargar el contenido de la Clase 16
-
-
-
Expresiones matemáticasConjunto de números, símbolos y operadores agrupados de acuerdo con las reglas de la matemática para representar un valor, una relación o una operación. Las expresiones matemáticas pueden ser algebraicas, aritméticas, lógicas, entre otras, y son fundamentales para la formulación y resolución de problemas matemáticos.AsíntotaLínea recta a la que una función se aproxima cada vez más a medida que la variable independiente tiende al infinito o a un punto específico.
-
DimensiónEn matemáticas, una dimensión es un número que describe el tamaño o la extensión de un objeto en un espacio determinado. Por ejemplo, una línea tiene una dimensión, un plano tiene dos dimensiones y un objeto tridimensional tiene tres dimensiones. Las dimensiones pueden extenderse a valores mayores en contextos más abstractos, como el espacio-tiempo en física o los espacios de alta dimensión en matemáticas aplicadas.Punto crítico en derivadasUn punto crítico de una función es un valor de la variable independiente en el cual la derivada de la función es cero o no está definida. En estos puntos, la función puede tener máximos, mínimos o puntos de inflexión. Los puntos críticos son fundamentales para el análisis de la optimización y el comportamiento de funciones en cálculo diferencial.
-
Integral definidaEs una integral que calcula el área bajo la curva de una función en un intervalo específico [a, b]. Se denota como ∫_a^b f(x)dx y proporciona el valor acumulado de la función entre los límites inferior (a) y superior (b).Integral indefinidaRepresenta una familia de funciones antiderivadas de una función dada. No incluye límites de integración y se denota como ∫f(x)" " dx, que es igual a F(x)+C, donde F(x) es la función antiderivada de f(x) y C es la constante de integración.
-
OfertaEn economía, la oferta se refiere a la cantidad de bienes o servicios que los productores están dispuestos a vender a diferentes precios durante un período determinado. La relación entre el precio y la cantidad ofrecida se ilustra mediante la curva de oferta, que generalmente tiene una pendiente positiva, indicando que, a mayores precios, se ofrece una mayor cantidad.DemandaEn economía, la demanda se refiere a la cantidad de bienes o servicios que los consumidores están dispuestos a comprar a diferentes precios en un período determinado. La relación entre el precio y la cantidad demandada se representa mediante la curva de demanda, que generalmente tiene una pendiente negativa, indicando que, a menores precios, mayor cantidad se demanda.
-
Función de demandaEs esencial comprender cómo varía la demanda de un producto en función del precio. La función de demanda, Qd=D(p), relaciona la cantidad demandada Qd con el precio p.CostoEn economía y negocios, el costo se refiere al valor monetario de los recursos utilizados para producir bienes o servicios. Esto incluye costos directos, como materiales y mano de obra, así como costos indirectos, como alquiler, servicios públicos y depreciación. Los costos pueden ser fijos, variables o mixtos, dependiendo de su comportamiento en relación con el nivel de producción.
-
GeoGebraEs un software de matemáticas dinámicas que combina geometría, álgebra, cálculo y estadísticas en una sola plataforma. Es ampliamente utilizado en la educación para enseñar y aprender matemáticas, facilitando la visualización interactiva de conceptos matemáticos y la resolución de problemas.ModeladoEn matemáticas y ciencias aplicadas, el modelado es el proceso de crear una representación abstracta de un sistema real utilizando ecuaciones matemáticas y algoritmos. El objetivo del modelado es analizar el comportamiento del sistema, hacer predicciones y probar hipótesis en un entorno controlado.
-
Asíntota verticalEs una línea vertical x = a, a la cual se aproxima una función cuando el valor absoluto de y tiende a infinito al acercarse x al valor a. Indica que la función no está definida en ese punto y presenta un comportamiento asintótico.Asíntota horizontalEs una línea horizontal y = b que representa el valor al que se aproxima una función cuando x tiende a infinito positivo o negativo. Indica el comportamiento de la función en los extremos del dominio.
-
Wolfram AlphaPlataforma de computación basada en la web que proporciona respuestas a preguntas formuladas en lenguaje natural mediante algoritmos avanzados y una vasta base de datos de conocimiento. Se emplea para realizar cálculos complejos, generar gráficos y obtener información precisa sobre una amplia variedad de temas.
-
Google ColabEs una herramienta basada en la nube que permite escribir y ejecutar código en Python directamente en el navegador. Proporciona acceso a recursos de computación gratuitos y facilita compartir y colaborar en proyectos, lo que potencia el aprendizaje y desarrollo de aplicaciones de datos y aprendizaje automático.PythonEs un lenguaje de programación de alto nivel, interpretado y de propósito general, conocido por su sintaxis clara y legible. Es ampliamente utilizado en el desarrollo web, análisis de datos, inteligencia artificial, automatización de tareas, entre otros, gracias a su extensa biblioteca estándar y su activa comunidad de desarrolladores.
-
MatplotlibBiblioteca de Python utilizada para crear visualizaciones estáticas, animadas e interactivas. Es particularmente útil para la generación de gráficos y diagramas en aplicaciones científicas y de ingeniería.NumPyBiblioteca fundamental para la computación científica en Python. Proporciona soporte para matrices y grandes conjuntos de datos multidimensionales, así como una colección de funciones matemáticas de alto nivel para operar con estos datos.
-
EncapsulamientoEs un principio de la programación orientada a objetos que restringe el acceso directo a algunos de los componentes de un objeto. Los atributos y métodos privados se ocultan y solo se pueden acceder a través de métodos públicos definidos en la clase. Esto mejora la modularidad y protege la integridad de los datos.Interfaz CompartidaEs un conjunto de métodos que diferentes clases pueden implementar, lo que permite que los objetos de estas clases sean tratados de manera uniforme. En la programación orientada a objetos, una interfaz define un contrato que las clases deben cumplir, asegurando que los métodos especificados en la interfaz estén presentes en las clases que la implementan.
-
-
Máximo relativoEs el punto en una función donde el valor de la función es mayor que en los puntos inmediatamente adyacentes. También conocido como máximo local, es un punto x=c tal que f(c)≥f(x) para todos los x cercanos a c.Mínimo relativoEs el punto en una función donde el valor de la función es menor que en los puntos inmediatamente adyacentes. También conocido como mínimo local, es un punto x=c tal que f(c)≤f(x) para todos los x cercanos a c.
-
Jupyter NotebooksEs un entorno interactivo basado en la web que permite a los usuarios crear y compartir documentos que contienen código en vivo, ecuaciones, visualizaciones y texto narrativo. Es ampliamente utilizado en análisis de datos, visualización y desarrollo de prototipos de código.Visual Studio CodeEs un editor de código fuente desarrollado por Microsoft, altamente extensible y que soporta una amplia variedad de lenguajes de programación. Es conocido por su interfaz intuitiva, integración con Git y un robusto ecosistema de extensiones que facilitan el desarrollo de software en múltiples plataformas.
-
BibliotecasConjunto de módulos y funciones predefinidos que pueden ser reutilizados en diferentes programas para realizar tareas específicas. En programación, las bibliotecas permiten simplificar el desarrollo al ofrecer herramientas ya creadas para manejar desde cálculos matemáticos hasta interfaces de usuario.Código:Conjunto de instrucciones escritas en un lenguaje de programación que una computadora puede interpretar y ejecutar para realizar una tarea específica. El código puede variar desde simples secuencias de comandos hasta complejos sistemas de software.
-
-
-
Enlaces de Reuniones
-
Grabaciones
-
-
-
¿Qué es PUCE CAFÉ?
PUCE Café es un espacio diseñado para conversar abiertamente con los participantes del aula virtual.
Ofrecemos algunos consejos para aprovechar al máximo la participación en PUCE CAFÉ
En este espacio, los invitamos a reflexionar y generar preguntas sobre los temas que hemos abordado en nuestra aula virtual. Esta es una excelente oportunidad para aclarar dudas, profundizar en conceptos y compartir inquietudes sobre los contenidos que hemos trabajado.
Pueden formular preguntas relacionadas con la incorporación de multimedia en Moodle, la organización y categorización de contenidos, así como las mejores prácticas para mejorar la accesibilidad y la experiencia de usuario en entornos de aprendizaje virtuales.
Recuerden que no hay preguntas incorrectas; cada aporte nos ayuda a enriquecer la experiencia de aprendizaje de todos. ¡Anímense a participar y plantear sus inquietudes!
Estamos aquí para apoyarles y responder sus preguntas, al igual que sus compañeros, quienes también pueden aportar sus conocimientos y experiencias.
¡Esperamos sus preguntas y comentarios!
-
-
-
Ficha Técnica
-
Idealización y Ejecución
Coordinación del Proyecto:
Javier CarreraCoordinación Administrativa:
Ana María PeñaCoordinación de Producción:
Fernando SpirituGenerador de contenido académicoNombre generador de contenido académico
ProducciónDiseño Multimedia
- Irvin Villavicencio
- Hans Yépez
Diseño Instruccional
- Salomé Palacios
- Christian Ñacato
Tecnología de la Información
- Juan Andrade
- Carlos Guamán
Soporte y ExperienciaSoporte en aulas
- Alex Tomarema
- Adrián Yépez
Acompañamiento
- Gabriela Yánez
Experiencia de usuario
- Katherine Ramos
Marketing y FinanzasFinanciero
- María José Maldonado
Marketing
- Camila Flor
-