-
Introducción
L
a optimización de precios y producción es un aspecto crucial en la gestión de negocios y la economía. Implica el uso de técnicas matemáticas y análisis para determinar los niveles óptimos de precios y cantidades de producción que maximicen el beneficio de una empresa.
A continuación, se exploran estos conceptos y sus aplicaciones.
-
5.1 Optimización5.2 Funciones matemáticas en aplicaciones prácticas
La optimización de precios y producción es un aspecto crucial en la gestión de negocios y la economía. Implica el uso de técnicas matemáticas y análisis para determinar los niveles óptimos de precios y cantidades de producción que maximicen el beneficio de una empresa.
A continuación, se exploran estos conceptos y sus aplicaciones.
5.1.1 Optimización de precios
La optimización de precios se refiere a la determinación del precio ideal de un producto o servicio que maximiza los beneficios de la empresa. Esto se logra considerando diversos factores, como los costos de producción, la demanda del mercado, la competencia y la percepción del valor por parte de los consumidores.
Función de Demanda: Es esencial comprender cómo varía la demanda de un producto en función del precio. La función de demanda,
,
relaciona la cantidad demandada con el precio .
La elasticidad-precio de la demanda, que mide la sensibilidad de la demanda ante cambios en el precio, es crucial para la fijación de precios.
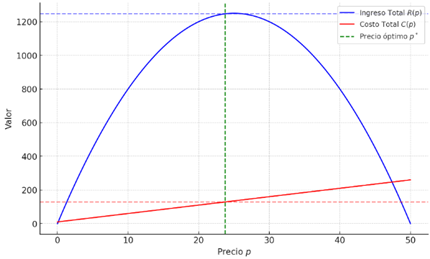
Figura 1: Maximización de beneficios
El gráfico muestra las funciones de ingreso total R(p) y costo total C(p) en función del precio p.Maximización del beneficio: El beneficio se maximiza cuando la derivada de la función de ingreso total menos la función de costo total con respecto al precio es igual a cero.
Matemáticamente, esto se expresa como:
Dondees el ingreso total y C(p) es el costo total (Pérez & Gómez, 2019).
La línea vertical verde punteada indica el precio óptimo p∗, donde la diferencia entre el ingreso total y el costo total (es decir, el beneficio) es máxima. Este punto se determina cuando la derivada del beneficio con respecto al precio es igual a cero, lo que significa que el ingreso marginal es igual al costo marginal en ese punto.
5.1.2 Optimización de la producción
La optimización de la producción implica determinar el nivel de producción que maximiza el beneficio o minimiza los costos. Esto se logra mediante el análisis de los costos marginales y los beneficios marginales.
- Costo marginal (CM): Es el costo de producir una unidad adicional. Se define como la derivada del costo total con respecto a la cantidad producida:
- Ingreso marginal (IM): Es el ingreso adicional obtenido por vender una unidad más de producto. Se calcula como la derivada del ingreso total con respecto a la cantidad vendida:
La regla para maximizar el beneficio es producir hasta el punto en que el ingreso marginal sea igual al costo marginal, es decir, IM=CM. Esto asegura que el costo de producir una unidad más no exceda el ingreso que genera (López & Torres, 2020).
En la práctica, la optimización de precios y producción se aplica en la fijación de precios de productos nuevos, en ajustes de precios en respuesta a cambios en el mercado y en la planificación de la capacidad de producción.
Por ejemplo, una empresa que fabrica dispositivos electrónicos puede usar estos principios para determinar cuántas unidades producir y a qué precio vender para maximizar los beneficios en diferentes regiones del mercado (Rodríguez & Sánchez, 2021).
En esta sección, revisaremos de manera simplificada las funciones que serán objeto de estudio en nuestra materia. Las funciones matemáticas son fundamentales en diversas áreas y se expresan mediante ecuaciones que relacionan variables.
Una función se define cuando a cada valor de entrada (generalmente x) le corresponde un valor de salida único (generalmente y). Gráficamente, una función es la representación visual de una ecuación.
Si una ecuación produce más de una salida para cada entrada, no define una función. Podemos imaginar una función como una "caja" que transforma una entrada en una salida específica.
Ejemplo de función
Considerando la ecuación:
4y−3x=8
Para definir y en función de x, despejamos:
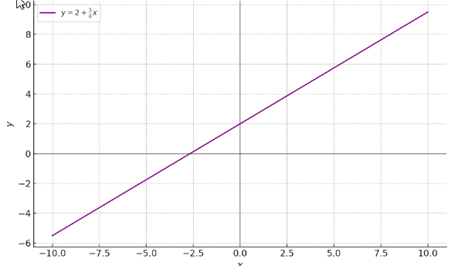
Figura 2: Gráfica de la función 𝑦=2+3/4𝑥
La pendiente positiva indica que la función crece a medida que x aumenta.Ejemplo de no función
Si tenemos:
Despejando y:
Aquí, y puede tomar dos valores para un mismo valor de x, por lo que no es una función.
Prueba gráfica
Para verificar si una ecuación es una función, utilizamos la prueba de la línea vertical. Si al trazar una línea vertical sobre la gráfica de la ecuación, esta intersecta la gráfica en más de un punto, entonces la ecuación no define una función.
Dominio de una función
El dominio de una función son los valores de x para los cuales la función está definida. Por ejemplo, para la función:
La expresión dentro de la raíz debe ser mayor o igual a cero:
El dominio de esta función es:
Aplicaciones en negocios
En el contexto de los negocios, se utilizan funciones específicas como las de costo, precio-demanda, ingresos y lucro.
Función de costo
C(x)=a+bx- a es el costo fijo.
- bx es el costo variable.
Función precio-demanda
P(x)=m-nxx es el número de ítems vendidos.
Función de ingresos
R(x)=x⋅P(x)- P(x) es la función de precio-demanda.
- R(x) es el ingreso total, que es el número de ítems vendidos por el precio de cada ítem.
Función de lucro
L(x)=R(x)-C(x)- L(x) es el lucro, que es la diferencia entre los ingresos y los costos.
Ejemplo práctico
Consideremos la función precio-demanda:
P(x)=75-3x
donde x está entre 1 y 20.
Para calcular los ingresos (R(x)):Completar una tabla de ingresos
Si vendemos x millones de ítems, los ingresos se calculan como:
- Para x=1:
- Para x=4:
- Y así sucesivamente hasta x=20.
Las funciones matemáticas son herramientas esenciales para analizar y resolver problemas en diversas áreas, incluidas las de los negocios.
- Costo marginal (CM): Es el costo de producir una unidad adicional. Se define como la derivada del costo total con respecto a la cantidad producida:
-
Profundiza más
Este video te ayudará a enfatizar sobre Funciones de Negocios ¡Accede aquí!
-
Actividades