-
Introducción
L
as funciones racionales son aquellas que se expresan como el cociente de dos polinomios.
Un ejemplo de función racional es:
En estas funciones, una característica importante son las asíntotas. Una asíntota es una línea a la cual la función tiende a aproximarse, pero nunca alcanza.
-
7.1 Uso de herramientas de cálculo diferencial e integral para visualización de costos, lucros e ingresos y cantidades marginales
Es la línea recta a la que una función se aproxima cada vez más a medida que la variable independiente tiende hacia el infinito o hacia un punto específico, pero que nunca llega a tocar.
Para visualizar esta definición, considere el siguiente gráfico de la función utilizando Python.
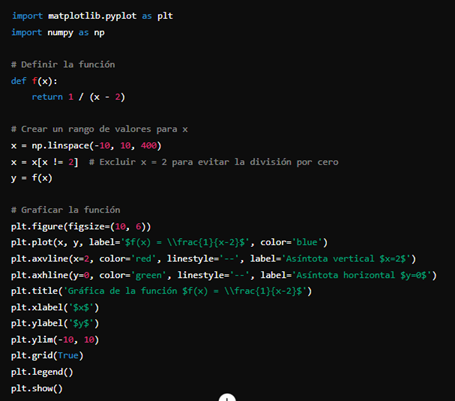
Figura 4: Gráfica de la función utilizando Python
Las asíntotas pueden ser verticales, horizontales u oblicuas, dependiendo de la naturaleza de la función y su comportamiento a largo plazo (Stewart, 2018).7.1.1 Tipos de asíntotas
Existen tres tipos principales de asíntotas:
Asíntotas verticales: Ocurren cuando el denominador de la función se iguala a cero y el numerador no se anula en esos puntos.
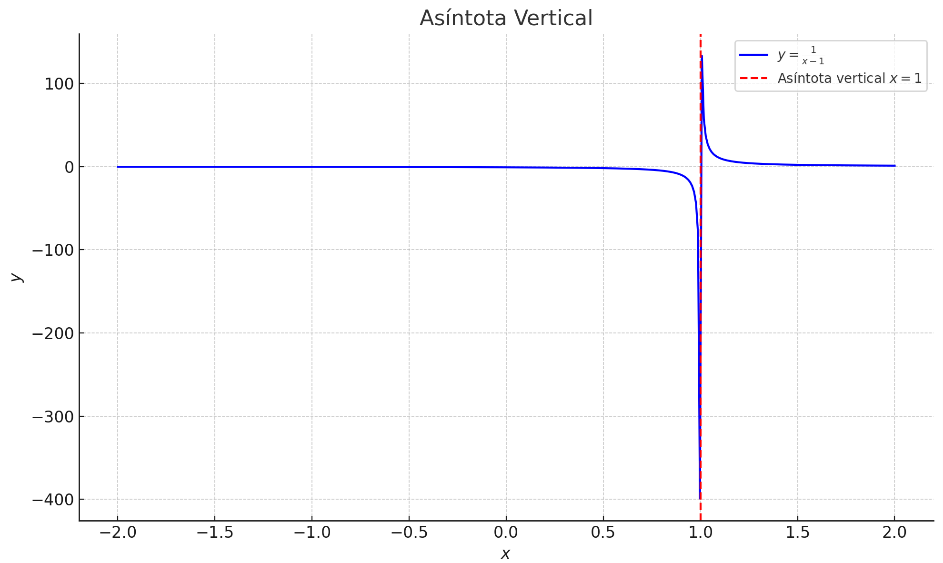
Figura 5: Asíntotas verticales
Gráfica extraída de GeogebraAsíntotas horizontales: Se determinan por el comportamiento de la función cuando x tiende al infinito.
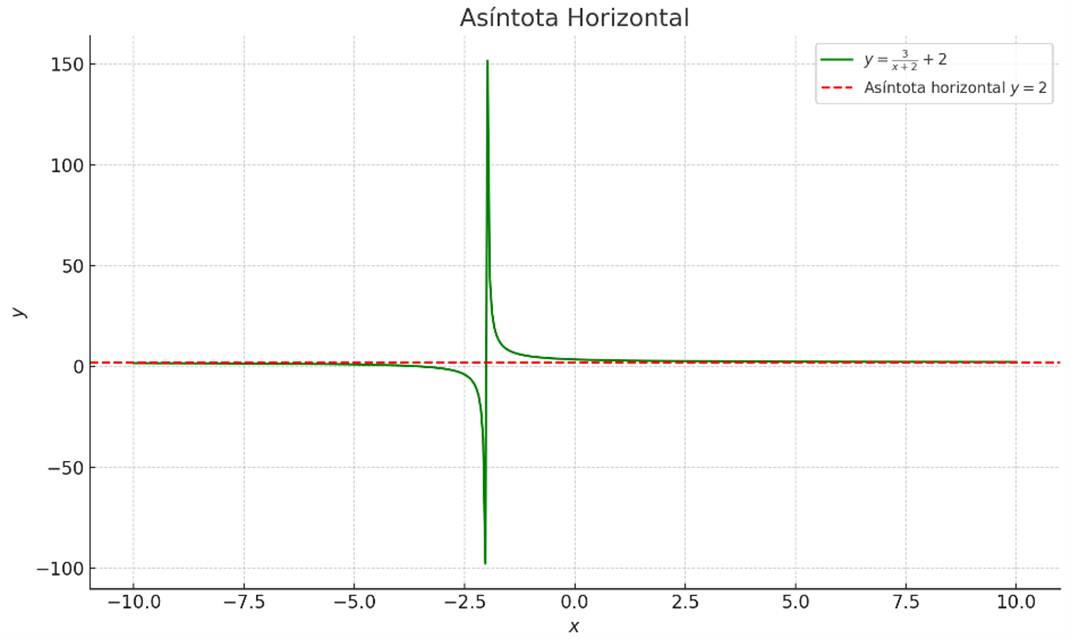
Figura 6: Asíntota Horizontal
Gráfica extraída de GeogebraAsíntotas inclinadas: Ocurren cuando el grado del numerador es mayor que el grado del denominador.
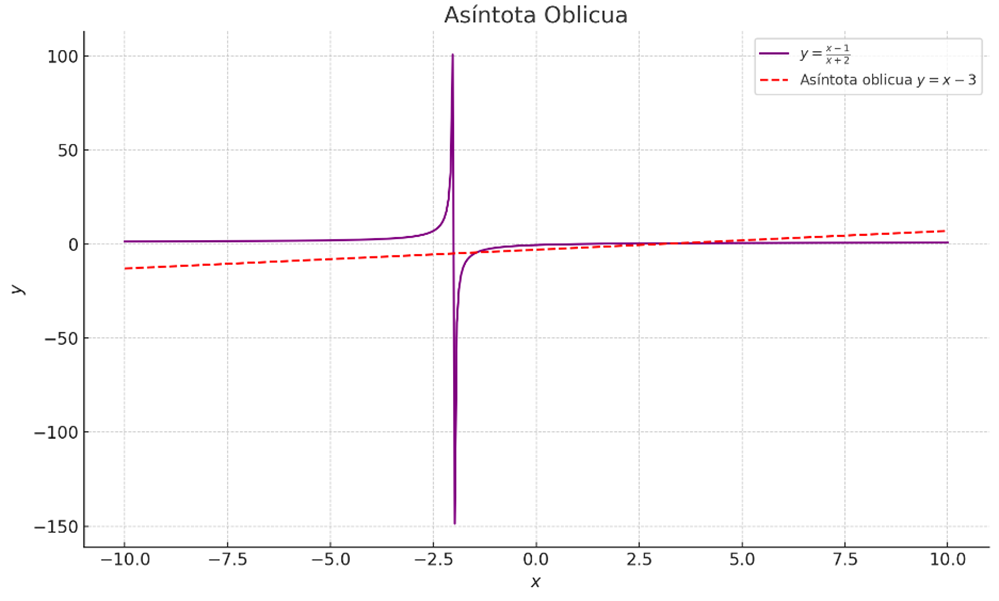
Figura 7: Asíntota oblicua
Gráfica extraída de GeogebraDeterminación de asíntotas
Para encontrar las asíntotas verticales, se iguala el denominador a cero y se resuelve para x. Si: entonces x = c es una asíntota vertical.
Para encontrar las asíntotas horizontales, se comparan los grados del numerador y del denominador:
- Si el grado del numerador es menor que el grado del denominador , entonces es la asíntota horizontal.
- Si los grados son iguales, la asíntota horizontal es: , donde y son los coeficientes principales de y , respectivamente.
- Si el grado del numerador es mayor que el grado del denominador, no existe asíntota horizontal.
La aplicación en negocios se puede ilustrar con un ejemplo. Supongamos que una compañía fabrica tablas de nieve con costos fijos de $200 por día y costos totales de $3800 por día al producir 20 tablas.
La función de costo es:
La función de costo promedio se define como:
Gráfico del costo promedio
Al graficar la función de costo promedio, se pueden determinar las asíntotas:
- Asíntota vertical: Se presenta en x = 0, ya que la función se indetermina en ese punto.
- Asíntota horizontal: Es y = 180, ya que, al dividir el coeficiente principal del numerador por el del denominador, se obtiene 180.
La asíntota horizontal en y = 180 indica que, a medida que la producción aumenta, el costo promedio por tabla tiende a ser $180.
Esto es crucial para entender que, aunque la producción se incremente significativamente, el costo promedio no superará los $180 por tabla.
Aquí tienes el texto corregido:
Ejercicio de aplicación
Supongamos una compañía fábrica tablas de nieve con los siguientes datos:
- Costos fijos: $200 por día.
- Costos totales: $3800 por día para 20 tablas.
- Función de costo:
- Función de costo promedio:
- Gráfico del costo promedio:
- Asíntota vertical: x=0
- Asíntota horizontal: y =180
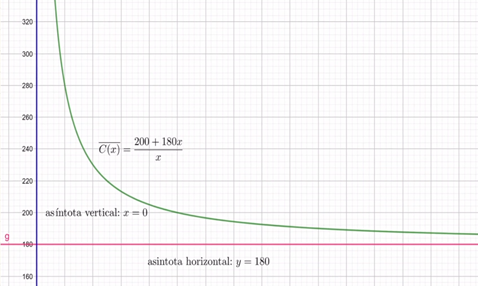
Figura 8: Gráfica del ejemplo
Las asíntotas en funciones racionales son fundamentales para entender el comportamiento a largo plazo de las funciones aplicadas en los negocios.En el caso del costo promedio de fabricación, sabemos que, al incrementar la producción, el costo promedio se estabilizará en $180 por tabla, lo que proporciona una guía importante para la toma de decisiones en producción y ventas.
-
Profundiza más
Este video te ayudará a enfatizar sobre Costo Promedio ¡Accede aquí!
-
Uso de herramientas de cálculo diferencial e integral para visualización de costos, lucros e ingresos y cantidades marginales