-
Introducción
Mostrar más Mostrar menosIntroducción
Queridos participantes,
¡Bienvenidos a esta emocionante aventura digital! Nos entusiasma ser parte de este viaje de aprendizaje, en el que descubrirán nuevas herramientas, adquirirán valiosos conocimientos y desarrollarán habilidades que les acompañarán a lo largo de su trayectoria.
Les invitamos a familiarizarse con la plataforma, conocer el curso y participar activamente.
¡Estamos aquí para apoyarlos en cada paso de este proceso!
¡Mucho éxito en este inicio!
El equipo de PUCE Virtual
-
Tutoriales
Sílabo
Manual del estudiante
-
Resultados de Aprendizaje y Criterios de Evaluación
Este curso trata de los fundamentos de la estadística e introduce al estudiante en el uso de herramientas tecnológicas apropiadas para su implementación. Este curso parte de conceptos básicos como poblaciones y muestra, la teoría del muestreo , tipos de variables, correlación y pruebas de hipótesis , diseño de experimentos y de distribuciones de tipo continuas y discretas.
En la segunda parte cubre la creación de modelos de predicción lineal simple, múltiple y logística. Los modelos son analizados usando múltiples métricas que permitan al analista perfeccionar el modelo ya sea ajustando las variables o mediante métodos de regularización.
RESULTADOS DE APRENDIZAJE
RDA 1: Identificar los conceptos de la Estadística Descriptiva e Inferencial que sustentan el desarrollo de procesos estadísticos.
- Criterio de evaluación 1: Realizar un análisis descriptivo del dataset mediante estadísticos y agregaciones que conduzcan a identificar y justificar variables pertinentes causantes de las demoras.
RDA 2: Calcular e interpretar estadísticos y parámetros para describir muestras y poblaciones.
- Criterio de evaluación 1: Identificar la distribución que siguen las variables estudiadas realizando diversas pruebas de hipótesis.
RDA 3: Analizar información contextual sobre hábitat, infraestructura y movilidad, mediante técnicas estadísticas descriptivas e inferenciales, para la adecuada toma de decisiones.
- Criterio de evaluación 1: Aplicar técnicas de regresión lineal y múltiple para crear modelos candidatos que consideren un subset de las variables identificadas anteriormente como pertinentes.
- Criterio de evaluación 2: Aplicar diversas técnicas para estimar la bondad de los modelos a fin de comparar ventajas y desventajas de cada uno de ellos.
PROYECTO FINAL
El proyecto final es la evaluación sumativa de los 3 retos, se considera como el entregable final de la asignatura.
Objetivo General
Desarrollar un modelo estadístico que permita predecir la probabilidad de demora en salida de vuelos de aeropuertos de NY, basado en condiciones ambientales y otros parámetros contenidos en el dataset.
Objetivos Específicos
- Realizar análisis exploratorio de los datos (EDA) tendientes a determinar la necesidad de implementar limpieza de datos, normalizaciones, imputaciones, o simplemente comprender su comportamiento por grupos o subgrupos mediante visualizaciones simples.
- Creación de pruebas de hipótesis y otras pruebas de contraste que permitan inferir el comportamiento de la población.
- Creación de modelos lineales o logísticos mediante el análisis de las variables que demuestren correlación y causación utilizando pruebas y visualizaciones adecuadas.
Descripción del Proyecto
El proyecto consiste en desarrollar un modelo de predicción que permita predecir la probabilidad de que un vuelo presente demoras en la salida del mismo, basado en información histórica y otras variables ambientales que pudieran tener un impacto.
Actividades
Reto Actividades Reto 1 - Realizar un análisis descriptivo del dataset
- Realizar agregaciones que conduzcan a identificar y justificar variables pertinentes causantes de las demoras
- Identificar actividades de preprocesamiento que deban implementarse sobre la data
Reto 2 - Realizar pruebas linealidad y normalidad para variables continuas
- Realizar pruebas pertinencia para variable nominales para variables nominales
- Realizar pruebas de hipótesis
Reto 3 - Aplicar técnicas de regresión lineal
- Aplicar técnicas de regresión logística
- Analizar el comportamiento de los modelos en base a predicción
Reto 4 - Obtener múltiples métricas como indicadores de la bondad los distintos modelos
- Aplicar técnicas de regresión logística
- Aplicar técnicas de comparación de modelos
Metodología (CRISP-DM)
- Entendimiento de la data: Incluye recolección de la data, análisis descriptivo de la data , EDA y verificación de la calidad de la misma
- Preparación de la data: determinar qué conjuntos de datos se utilizarán y documentar los motivos de inclusión o exclusión, limpieza de datos, transformaciones que deben hacerse sobre los datos
- Modelado: Revisar las técnicas de modelado y seleccionar la más apropiada, diseño de subsets de prueba y validación, construcción de modelos y validación
- Cada reto corresponde a una entrega parcial del proyecto.
Criterios de Evaluación del proyecto
Criterio Ponderación Detalle Funcionalidad completa 40% Cumplimiento de los 4 retos Documentación del código mediante archivos RMD o Jupyter 35% Uso de funciones, bucles y condicionales de manera eficiente. Manejo de archivos 25% Eficiencia del modelo en la predicción Cronograma de entregables del Proyecto
Semana Reto Entregable Contenido 4 Reto 1 Análisis exploratorio completo Estadística descriptiva de los datos y visualización de los mismos 8 Reto 2 Pruebas de hipótesis y pruebas de contraste Desarrollo de la pruebas y entendimiento de los resultados 12 Reto 3 Modelos Desarrollo de modelos y análisis inicial de la calidad de este 16 Reto 4 Comparación de modelos Técnicas aplicadas para comparar los distintos modelos candidatos Retos de aprendizaje de la asignatura
RETO 1: Análisis descriptivo del dataset mediante estadísticos y agregaciones que conduzcan a identificar y justificar variables pertinentes causantes de las demorasObjetivo: Analizar todas las variables del dataset, establecer sus principales estadísticos, visualizar la data.
Indicaciones:
- Entender los distintos tipos de datos:
- Variables cuantitativas: discretas y continuas
- Variables cualitativas: nominales y ordinales
- Medidas de tendencia central:
- Distintos tipos de medias
- Máximos, mínimos y rangos
- Medidas de dispersión:
- Cuantiles
- Varianzas y distribución
RETO 2: Identificar la distribución que siguen las variables estudiadas realizando diversas pruebas de hipótesisObjetivo: Entender las variables en términos de distribuciones de distinto tipo.
Indicaciones:
- Identificación del tipo de variables:
- Cualitativas y cuantitativas
- Establecer relaciones entre variables:
- Aplicar medidas de correlación y covarianza
- Visualizar las relaciones
- Aplicación de pruebas de contraste:
- Establecer hipótesis sobre la población
- Hipótesis de un lado y de dos lados
RETO 3: Aplicar técnicas de regresión lineal y múltiple para crear modelos candidatos que consideren un subset de las variables identificadas anteriormente como pertinentesObjetivo: Crear modelos basados en distintos subsets de variables.
Indicaciones:
- Aplicar regresiones lineales múltiples o regresiones logísticas
- Analizar resultados iniciales de residuos
- Analizar incertidumbre de coeficientes
- Validación de los modelos mediante técnicas de validación cruzada:
- Uso de particiones nfold
- Obtener métricas de rendimiento:
- R², R² ajustado
- Error estándar residual
RETO 4: Aplicar diversas técnicas para estimar la bondad de los modelos a fin de comparar ventajas y desventajas de cada uno de ellosObjetivo: Comparar diversos modelos.
Indicaciones:
- Aplicar métricas derivadas del likelihood:
- Estimadores y deviances
- Aplicar métricas derivadas de cross-validación:
- Delta
- Aplicar ANOVA:
- Análisis del estadístico F
-
Índice
Resultados de aprendizajeClasesResultado de aprendizaje 1
Identificar los conceptos de la Estadística Descriptiva e Inferencial que sustentan el desarrollo de procesos estadísticos
Resultado de aprendizaje 2
Calcular e interpretar estadísticos y parámetros para describir muestras y poblaciones
Resultado de aprendizaje 3
Analizar información contextual sobre hábitat, infraestructura y movilidad, mediante técnicas estadísticas descriptivas e inferenciales, para la adecuada toma de decisiones
-
Vencimiento: martes, 4 de noviembre de 2025, 23:00
Mostrar más-
-
RETO 1: Análisis descriptivo del dataset mediante estadísticos y agregaciones que conduzcan a identificar y justificar variables pertinentes causantes de las demoras
Objetivo: Analizar todas las variables del dataset, establecer sus principales estadísticos, visualizar la data.
Indicaciones:
- Entender los distintos tipos de datos:
- Variables cuantitativas: discretas y continuas
- Variables cualitativas: nominales y ordinales
- Medidas de tendencia central:
- Distintos tipos de medias
- Máximos, mínimos y rangos
- Medidas de dispersión:
- Cuantiles
- Varianzas y distribución
Actividades
- Realizar un análisis descriptivo del dataset
- Realizar agregaciones que conduzcan a identificar y justificar variables pertinentes causantes de las demoras
- Identificar actividades de preprocesamiento que deban implementarse sobre la data
-
Introducción
En esta clase, iniciaremos con los fundamentos de la estadística y su propósito en la Ciencia de Datos, así como con la introducción del estudiante a las herramientas tecnológicas que se utilizarán para su implementación. Específicamente, en la primera parte, revisaremos el uso de R y RStudio, y su aplicación en distintas fases de la estadística.
En la segunda parte, abordaremos la terminología básica, los tipos de variables utilizados en el análisis de las medidas de tendencia central y las medidas de dispersión. También introduciremos gráficos que permitan entender de mejor manera los diversos estadísticos.
SERIES TEMPORALES
Conocida también como serie cronológica. Es la sucesión de observaciones cuantitativas ordenadas en el tiempo de un fenómeno. Los datos tienen un orden que no es posible variar. La información puede ser mensual, trimestral, anual o de cualquier otro intervalo temporal.
VARIABLE ALEATORIA
Conocida también como variable estocástica o probabilística. Es la característica considerada en un experimento aleatorio cuyo valor de ocurrencia solo puede saberse con exactitud una vez observado.
-
1.0. Terminología Básica
En primer lugar, empecemos indicando que es estadística: Existen múltiples definiciones de la estadística, posiblemente una por cada autor, a continuación, veremos algunas de las mejores definiciones:
- La estadística es la ciencia que estudia cómo debe emplearse la información y cómo dar una guía de acción en situaciones prácticas que entrañan incertidumbre., la cual implica su recolección, clasificación, síntesis, organización, análisis e interpretación, para la toma de decisiones frente a la incertidumbre. Gutiérrez 1998
- La estadística es la rama del conocimiento humano que tiene como objeto el estudio de ciertos métodos inductivos aplicables a fenómenos susceptibles de expresión cuantitativa. (López, 2020)
De estas definiciones podemos extraer los siguientes detalles:
De acuerdo con Gutierrez, (2007), debemos notar que hace referencia a la “incertidumbre”. Esto es correcto, aunque, contrario a lo que se piensa, la estadística no es una ciencia matemática cuyos resultados sean siempre exactos. En realidad, las operaciones estadísticas nos muestran valores dentro de un rango. No podemos asegurar cuál es el valor real, pero sabemos que estará dentro de un intervalo determinado.
Notaremos que la estadística abarca desde funciones que tiene que ver con la recolección de la información, su tratamiento y análisis de lo que nos está mostrando.
Por último, de acuerdo con López (2020), la estadística es una ciencia de carácter inductivo, lo que significa que se basa en los datos para tomar decisiones, a diferencia de los estudios deductivos, en los cuales se conoce de antemano lo que se intenta demostrar.
Existen tres ramas (o si se quiere tres etapas) de la estadística, cada una comprende una serie de técnicas y funciones que permiten contestar las siguientes preguntas:
¿Qué pasó? ¿Qué está pasando?
¿Qué pasará si seguimos de la misma manera en el futuro?
¿Qué podría pasar si se alteran las condiciones del negocio?
En esta clase, trataremos de responder la primera pregunta. El conjunto de métodos y procedimientos que nos ayudan a contestarla se denomina estadística descriptiva.
Estadística Descriptiva: Es la rama de las matemáticas que recolecta, presenta y caracteriza un conjunto de datos (por ejemplo, edad de una población, altura de los estudiantes de una escuela, temperatura en los meses de verano, etc.) con el fin de describir apropiadamente las diversas características de ese conjunto. Por lo tanto, la estadística descriptiva se apoya o trabaja en base a variables que describen un proceso, evento, negocio, una enfermedad, etc.
Puede haber múltiples variables en un caso de estudio y estas variables pueden ser de distinta naturaleza. De la misma manera que el éxito de una aplicación es haber realizado un correcto análisis de las propiedades de los objetos y clases, el éxito de la estadística es haber recolectado todos los factores que afectan al proceso, evento, negocio, etc.
Tipos de Datos
Para iniciar con la estadística descriptiva, es importante mencionar que existen varios tipos de datos. Comúnmente, asociamos la palabra "dato" con una variable numérica, pero esto no siempre es el caso. Existen diversos tipos de datos dentro del análisis estadístico.
Empezaremos por catalogar dos grandes grupos de tipos de datos:
- Variables cuantitativas: Las observaciones se expresan numéricamente. Dentro de esta categoría podemos ubicar algunas variantes:
- Variables continuas: Son aquellas que pueden tomar cualquier valor, con cualquier cantidad de decimales, en algunos casos podrían estar acotadas o dentro de un rango. Ejemplo: π = 3.14159.
- Variables discretas: Pueden tomar determinados valores numéricos únicamente, por ejemplo, la edad de una persona. Un caso particular de esta es la data binaria que solo puede tomar dos valores: Verdadero/Falso.
- Series de Tiempo: Es una subclase de cuantitativa representada por listas o vectores que representan el valor de la variable a través del tiempo, por ejemplo, temperatura de la ciudad durante el año.
- Ratio o Razón: Relación entre dos variables numéricas y generalmente se expresa en términos de porcentajes, por ejemplo, tasa de cambio de una moneda.
- Intervalo: Variables que se hallan dentro de un rango. Esto es muy utilizado por ejemplo en secuencias en R o rangos en Python, ejemplo: secuencia de conteo del 1 al 10, en R representado por la función seq (1::10).
- Variables cualitativas: A este grupo pertenecen las variables que describen características que pueden presentarse en los elementos que conforman el conjunto de datos. En R también se les conoce como variables tipo factor. En esta categoría podemos ubicar los siguientes casos:
- Variables categóricas: Son variables que se consideran clasificadoras o calificadoras, ya que catalogan los elementos en grupos, conjuntos o categorías. Se conocen como dicotómicas aquellas que solo pueden adoptar dos valores diferentes, y como politómicas las que poseen un número de valores mayor a dos.
- Variables nominales: Nombres o clasificaciones que se utilizan para datos en categorías, por ejemplo, país, género, color, que por su naturaleza no pueden ser ordenadas.
- Variables ordinales: Datos que si bien no son numéricos, sí nos dan un sentido de prioridad. Por ejemplo: pequeño, mediano, grande; variables que pueden ser ordenadas.
La siguiente figura explica la clasificación:
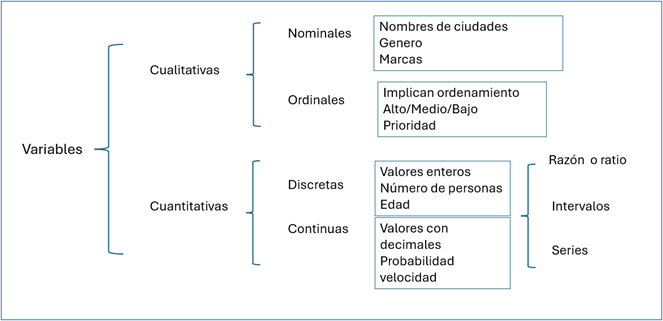
Figura 1: Taxonomía de las variables.
Creación autor: Alfonso Prado.estadistica

-
1.1 Medidas de tendencia central
Como mencionamos anteriormente, el propósito de la estadística descriptiva es describir los datos. Existen múltiples herramientas para ello. A continuación, exploraremos algunas de las más comunes.
1.1.1 Promedio
Promedio: Es el valor central de un conjunto de datos y nos indica cuál es el valor esperado para una , considerando todas las posibilidades. En R, la función utilizada para calcularlo es mean(), cuya sintaxis y fórmula se describen en la siguiente figura.
Figura 2
Referencia: Función mean sintaxis y fórmula . www.rdocumentation.orgFigura 2: Función mean sintaxis y fórmula . www.rdocumentation.org
La función acepta los siguientes argumentos:
- x: representa el vector que contiene los datos.
- trim: Es la fracción (0 a 0.5) de observaciones que se deben recortar de cada extremo de
xantes de calcular la media. . Los valores de recorte que se encuentren fuera de ese rango se toman como el punto final más cercano y es útil en caso de que el dataset tenga valores atípicos. - na.rm: Un valor lógico que indica si los valores NA deben eliminarse antes del cálculo. En R cuando un valor de una variable figura como NA indica que no se ha ingresado dicho valor y es diferente al caso de asumir que su valor es cero o nulo. La importancia de este argumento radica en que cualquier operación que se realiza sobre un vector que contiene al menos un valor NA dará como resultado NA.
Si analizamos la fórmula de la función mean(), veremos que todos los valores tienen un peso igual. Esto podría no ser apropiado en algunos casos. Para esto utilizamos la media ponderada:
Media ponderada:
La media aritmética ponderada es similar a una media aritmética, excepto que en lugar de que cada una de las observaciones contribuyan igualmente al promedio final, algunas contribuyen más que otras. Podemos obtener la media ponderada usando el paquete DescTools. La función y formula se muestran en la figura 3..
Figura 3: Media Ponderada sintaxis y fórmula
Referencia: Media Ponderada sintaxis y fórmula. www.rdocumentation.orgFigura 3: Media Ponderada sintaxis y fórmula
Referencia: Media Ponderada sintaxis y fórmula. www.rdocumentation.orgNote que la función es Mean con mayúscula, en R mayúsculas no son igual que minúsculas. Los argumentos son similares a la función mean, excepto que se introduce el argumento weights, que representa los pesos de cada una de la observaciones
- weights: representa los pesos de cada una de las observaciones.
Media geométrica
Esta es un tipo de media que se usa generalmente en ambientes financieros debido a que su resultado es un poco más conservador. Su valor se obtiene mediante la raíz n de la multiplicación de los valores de las observaciones. Existen muchos paquetes que proveen esta funcionalidad, en nuestra clase utilizaremos la función gm() del paquete rob.compositions . Debido a que la multiplicación de los valores de las observaciones puede arrojar valores muy grandes alternativamente se puede calcular como la constante de Euler (e=2.7182) elevado a la potencia de la media de los logaritmos neperianos de la data, de esta forma garantizamos que no se producirá un “overflow” en su cálculo. Su función y fórmula se muestran en la figura 4..
Figura 4: Media geométrica, sintaxis y fórmula
Figura 4: Media geométrica, sintaxis y fórmula
1.1.2 Moda
Moda: Esta función permite calcular el o los valores más repetidos dentro de un conjunto de datos. En lenguaje R, el paquete modeest ofrece diversas funciones para estimar la moda, destacándose entre ellas la función mlv(), la cual retorna un vector numérico con el valor o los valores más frecuentes. Esta función admite varios métodos de estimación, lo que proporciona flexibilidad según las características de los datos analizados. La sintaxis correspondiente se muestra en la Figura 5.
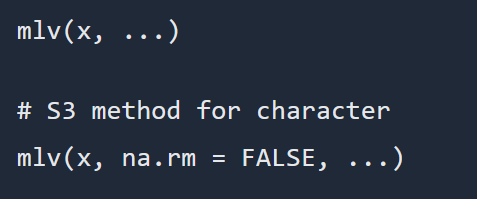
Figura 5: Sintaxis de la función mlv
Referencia: Moda sintaxis y fórmula . www.rdocumentation.org .Figura 5: Sintaxis de la función mlv
Referencia: Moda sintaxis y fórmula . www.rdocumentation.org .
mlv es una función genérica para estimar la moda de una distribución univariante. Se proporcionan diferentes métodos, el más común es “mfv” que significa el valor más frecuente.
-
1.2 Medidas de dispersión
Se llama dispersión de los datos a la variabilidad que existe entre ellos. Cuando tenemos un set de datos de una variable aleatoria, se podría pensar que estos podrían asumir cualquier valor. Sin embargo, en la realidad, cuando se analiza un fenómeno, los datos tienden a estar más o menos agrupados alrededor de la media. Existen varias funciones que nos permiten cuantificar esta dispersión.
1.2.1 Percentiles
Cuantiles: Los cuantiles nos dan una primera idea de la distribución de los valores. Un cuantil o percentil indica qué porcentaje de los datos se encuentra por debajo de un cierto valor de la variable bajo análisis. Por ejemplo, el cuantil del 50 por ciento es lo mismo que la mediana. R tiene algunas funciones convenientes para ayudar a observar los cuantiles.
La función quantile() puede proporcionarle cualquier cuantil que desee. Para ello, se utiliza el argumento
probscomo un número fraccionario. Por ejemplo, para obtener el cuantil del 20%, se utilizará 0.20 como valor de este argumento. Este argumento también puede recibir un vector como valor, por lo que es posible obtener los cuantiles de 5% y 95% simultáneamente.Es importante mencionar que existen distintos algoritmos para el caso de variables discretas y continuas, y que no todas las herramientas informáticas utilizan el mismo algoritmo. Esto puede ser relevante e incluso desconcertante si se está trabajando con diferentes herramientas a la vez, ya que podrían proporcionar resultados distintos.
Los algoritmos se numeran del 1 al 3 para variables discretas, como fechas o factores ordenados, y del 4 al 9 para variables continuas. El algoritmo se define mediante el argumento type, siendo 7 el valor por defecto.
La figura 6 muestra la sintaxis de la función quantile(), así como las fórmulas aplicables a los distintos métodos.
Aprende más
Para conocer más sobre el tema, puedes leer el siguiente artículo ¡Accede aquí!
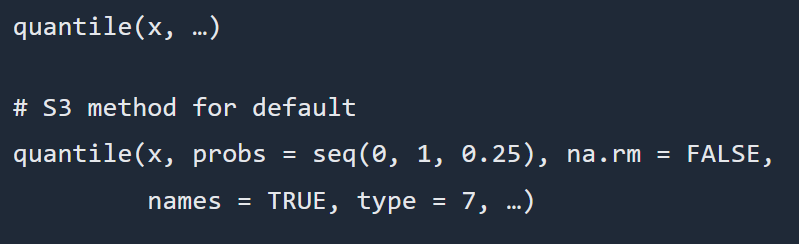
Figura 6: Sintaxis función quantile
Referencia: Quantile sintaxis. www.rdocumentation.orgFigura 6: Sintaxis función quantile
Referencia: Quantile sintaxis. www.rdocumentation.org
1.2.2 Varianza
Varianza: Es una medida de dispersión que representa la variabilidad de una serie de datos respecto a su media. Una serie de datos podría tomar un número infinito de valores, pero en la práctica, cuando se analiza un parámetro de interés, los datos tienden a estar dentro de un rango más o menos disperso. La varianza indica la medida de esta dispersión.

Figura 7: Función y fórmula de la varianza
Referencia: Varianza sintaxis y fórmula. www.rdocumentation.orgFigura 7: Función y fórmula de la varianza
Referencia: Varianza sintaxis y fórmula. www.rdocumentation.org
1.2.3 Desviación
Desviación estándar: Representa la raíz cuadrada de la varianza. El símbolo σ (sigma) se utiliza frecuentemente para representar la desviación estándar de una población, mientras que s se utiliza para representar la desviación estándar de una muestra.
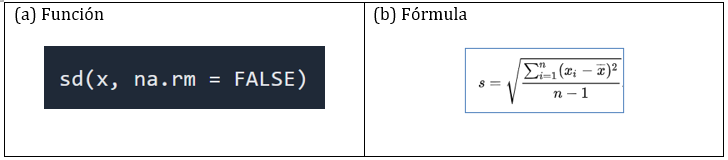
Figura 8: Desviación estándar función y fórmula
Referencia: Desviación estándar función y fórmula. www.rdocumentation.orgFigura 8: Desviación estándar función y fórmula
Referencia: Desviación estándar función y fórmula. www.rdocumentation.org
1.2.4 Cómo visualizar la dispersión de los datos
ggplot2 es un paquete de visualización de datos para el lenguaje R. Es un esquema general para la visualización de datos que divide los gráficos en componentes semánticos en una modalidad de capas. ggplot2 es un paquete mejorado de los gráficos base en R (plot).
Forma parte del paquete Tidyverse, un sistema para la manipulación, exploración y visualización de datos que comparten una filosofía de diseño común. Los paquetes del Tidyverse están destinados a ser usados por estadísticos y científicos de datos. Básicamente, tidyverse trata sobre las conexiones entre las herramientas que hacen posible el flujo de trabajo.
ggplot2 permite generar una gran cantidad de tipos de gráficos. Las gráficas de dispersión son más útiles para mostrar la relación entre dos variables continuas, o cuando una entidad está compuesta por dos valores. Para visualizar la dispersión utilizaremos la función geom_point, cuya sintaxis se muestra en la figura 9.
Información adicional sobre ggplot2, el siguiente enlace describe la operación básica del paquete (enlace).
Aprende más
Para conocer más sobre ggplot2, puedes leer el siguiente artículo ¡Accede aquí!
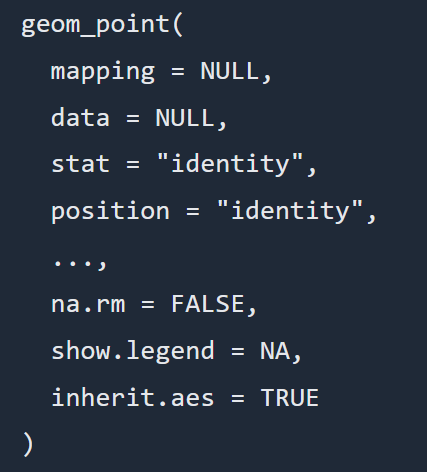
Figura 9
Referencia: Sintaxis de la función geom_point, www.rdocumentation.orgFigura 9
Referencia: Sintaxis de la función geom_point, www.rdocumentation.org
Donde el argumento mapping permite indicar qué variables del dataset son asignadas a cada eje. El argumento data, por supuesto, corresponde al dataframe que contiene los datos. El argumento position permite alterar la posición de las observaciones en situaciones de sobre-trazado, con el fin de mejorar la visualización.
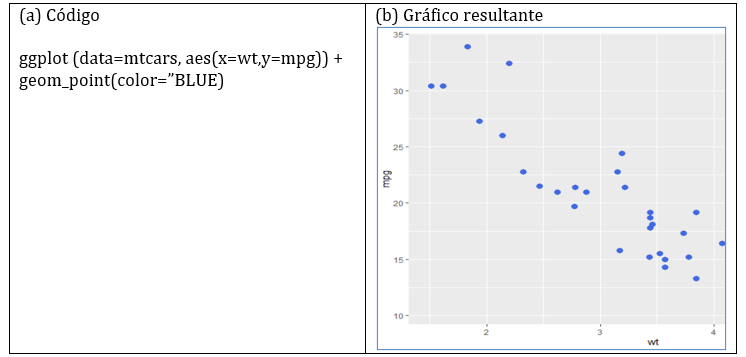
Figura 10: Código y visualización de la dispersión del dataset mtcars
Creación autor: Alfonso PradoFigura 10: Código y visualización de la dispersión del dataset mtcars
Creación autor: Alfonso Prado
Profundiza más
Este recurso te ayudará a enfatizar sobre Diagramas de dispersión ¡Accede aquí!
-
-
-
Actividades
-
Hacer un envío
-
Hacer intentos: 1
-
-
-
Introducción
En esta clase, iniciaremos con el estudio de las relaciones entre variables; específicamente, trataremos sobre distintas funciones y algoritmos para medir la correlación y covarianza entre dos o más variables, así como técnicas para visualizar la correlación.
Un tema importante en la estadística es tratar de entender cómo se relacionan las variables entre sí. Para ello, introduciremos los temas de correlaciones, covarianza y causación. Lo anterior estará apoyado por el conocimiento del marco general del lenguaje R y la interfase RStudio, los mismos que se usarán en los laboratorios propuestos y que reforzarán el aprendizaje incorporando algunos enlaces externos. Un tema particular en este caso es la determinación de la existencia de relaciones espurias.
CORRELOGRAMA
Es un gráfico que permite apreciar las autocorrelaciones r₁, r₂, ..., rₖ mediante el cual se identifican si los datos de una serie de tiempo tienen las siguientes características: estacionalidad, aleatoriedad, tendencia y estacionariedad.
PRUEBA CHI CUADRADO
De acuerdo con Ramírez-Alan (2016), “El test Χ² considera la hipótesis nula (H₀) de que las variables son independientes. Si esto es verdad, la frecuencia de ocurrencia debería estar dada por la cantidad de casos totales multiplicada por la probabilidad esperada”. En el ejemplo anterior, si la probabilidad de compra es igual para los 3 niveles socioeconómicos (πᵢⱼ = 33%), entonces si se han vendido 1000 ítems, estos deberían estar distribuidos en las 3 categorías (n*πᵢⱼ = 1000*0.33), valor conocido como μᵢⱼ.
Pero si Hₐ está en lo correcto, va a existir una diferencia entre la frecuencia observada (ηᵢⱼ) y la esperada (μᵢⱼ), indicando que existe algún fenómeno por detrás que influencia la frecuencia observada. La prueba Χ² calcula esta diferencia de la siguiente forma
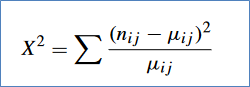
-
Reto #2
2. Relacionamiento de variables
En la clase anterior, revisamos la clasificación de las variables desde el punto de vista de los tipos de datos; es así que mencionamos la distinción entre variables continuas y discretas, o variables nominales y ordinales.
Ahora presentaremos otra clasificación basada en la relación que se observa entre estas variables, en base al concepto de causa-efecto. La idea es entender si una variable es la causante de que otra variable cambie de valor.
Variables Predictoras y de Respuesta
Predictoras (anteriormente llamadas variables independientes) son variables que representan un argumento para obtener un efecto sobre otra variable.
Variables de Respuesta (anteriormente llamadas dependientes) son variables que obtienen su valor en base a variables predictoras.
Para entender mejor el tema imagine la representación de una función matemática en un plano cartesiano Y = f(x), donde la variable Y tomará un valor derivado de la variable X y no al revés.
Por ejemplo, en R tenemos un dataset llamado
mtcars, el cual contiene una decena de variables relacionadas con características de vehículos. Dos de estas características son:disp(que representa el volumen de los cilindros de un vehículo, establecido en centímetros cúbicos) ympg(el rendimiento o millas por galón), y queremos entender qué tipo de relación tiene este par de variables.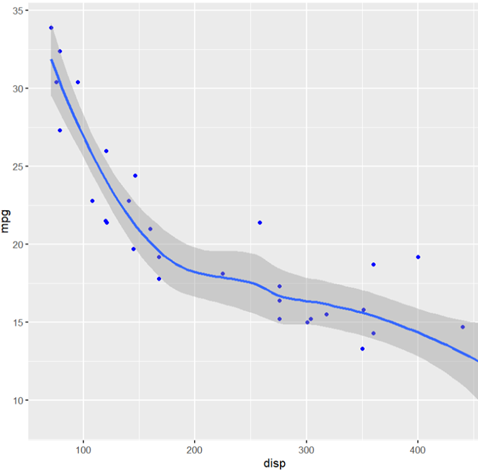
Figura 1: Relación disp vs mpg
Creación de autor: Alfonso PradoFigura 1: Relación disp vs mpg
Creación de autor: Alfonso Prado
De la Figura 1 notamos que a medida que los cc. del motor aumentan, el rendimiento de consumo de gasolina disminuye.
En estadística, una relación monótona entre dos variables se refiere a un escenario en el que un cambio en una variable generalmente se asocia con un cambio en una dirección específica en otra variable.
Hay dos tipos de relaciones monótonas:
- Monotónica positiva: Cuando el valor de una variable aumenta, el valor de la otra variable tiende a aumentar también.
- Monotónica negativa: Cuando el valor de una variable aumenta, el valor de la otra variable tiende a disminuir.
- No monotónica: Si dos variables generalmente no cambian en la misma dirección, entonces se dice que tienen una relación no monótona.
Cuando analizamos la relación entre dos variables, también es importante distinguir entre un comportamiento lineal y no lineal. En algunos casos, podemos observar que dicha relación es monotónica positiva solo en cierto rango y luego pasa a ser monotónica negativa, o simplemente se estabiliza en cierto valor.
En base a estos dos conceptos podemos establecer las siguientes posibilidades:
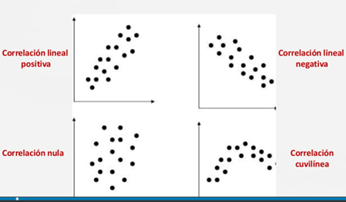
Figura 2: Distintos tipos de correlaciones
Figura 2: Distintos tipos de correlaciones

-
2.1 Medición de la correlación y covarianza
Una vez que hemos entendido la relación entre dos variables, nos interesa cuantificar qué tan fuerte es dicha relación; para esto, existen distintos métodos para cuantificarla. Estos métodos podemos distinguirlos en dos clases.
PRUEBAS PARAMÉTRICAS Y NO PARAMÉTRICAS
La diferencia principal entre estos dos tipos es su base matemática para el cálculo. Las pruebas paramétricas se basan en el entendimiento de la distribución de las variables. Este concepto lo veremos más adelante en el curso. Por el momento, diremos que las pruebas paramétricas asumen una cierta distribución.
Ventajas de las Pruebas Paramétricas
- Tienen más poder de eficiencia.
- Más sensibles a los rasgos de los datos recolectados.
- Menos posibilidad de errores.
- Dan estimaciones probabilísticas bastante exactas.
2.1.1 Correlación
Para el cálculo de la correlación tenemos las siguientes pruebas:
Correlación de Pearson: mide una dependencia lineal entre dos variables (X, Y). Es una prueba de tipo paramétrica. Se puede usar solo cuando X e Y son de distribución normal (esto lo veremos más adelante).
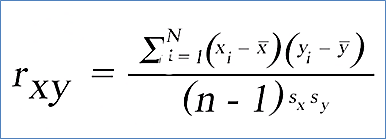
Figura 3: Fórmula de la Correlación de Pearson
Figura 3: Fórmula de la Correlación de Pearson
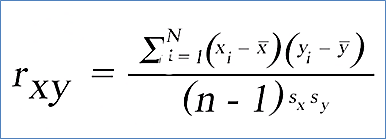
Donde:
- ̄X y ̄Y representan la media del vector X y Y respectivamente.
- Sx y Sy representan las desviaciones estándar de X y Y respectivamente.
- n es la cantidad de observaciones.
Correlación de Kendall y Spearman, son coeficientes de correlación basados en rangos (no paramétricos): Las pruebas no paramétricas son aquellas que se encargan de analizar datos que no tienen una distribución particular y se basan en hipótesis, pero los datos no están organizados de forma normal. Aunque tienen algunas limitaciones, cuentan con resultados estadísticos ordenados que facilita su comprensión.
Para el cálculo de la correlación usaremos la función
cor()cuya sintaxis se muestra en la siguiente figura.
Figura 4: Sintaxis de la función cor
Referencia: Sintaxis de la función, www.rdocumentation.orgFigura 4: Sintaxis de la función cor
Referencia: Sintaxis de la función, www.rdocumentation.org
Retorna el coeficiente de correlación.
Es importante mencionar que
cor()puede tomar 2 vectores (X y Y) o un dataframe completo que puede tener múltiples columnas, por lo tanto, si la data es muy extensa su resultado será una matriz de correlaciones entre todos los vectores deldata.frame.Esta matriz tiene las siguientes características:
- La matriz es simétrica, la correlación entre a y b es la misma que entre b y a.
- Los valores de la correlación varían entre -1 y 1; el signo indica si la relación es monotónica negativa o positiva, y el valor absoluto indica qué tan fuerte es la relación.
- La diagonal es siempre 1 (una variable siempre se correlaciona consigo misma).
Es recomendable limitar las columnas que intervienen mediante “subsetting”, es decir, seleccionando un subconjunto de columnas de interés.
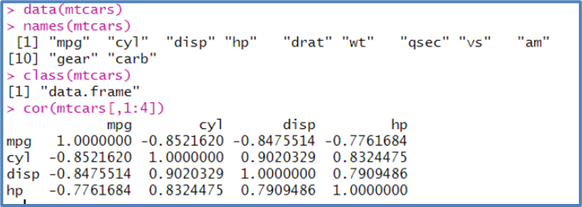
Tabla 1: Matriz de correlación en el dataset mtcars
Creación de autor: Alfonso PradoTabla 1: Matriz de correlación en el dataset mtcars
Creación de autor: Alfonso Prado
Cuando la matriz es pequeña como en la tabla anterior, analizar las relaciones es simple, pero cuando se tiene decenas o centenas de variables se torna difícil. En este caso recurrimos a la visualización.
Por ejemplo, utilizando el dataset
economics, este contiene las siguientes columnas:- Pce: Gastos de consumo personal
- Pop: Población total, en miles
- Psavert: Tasa de ahorro personal
- Uempmed: Duración media del desempleo, en semanas
- Unemploy: Número de desempleados en miles
Utilizando
ggplot, podemos crear un mosaico cuyos colores representan la fuerza de la correlación. Colores fuertes representan una correlación alta, y colores neutros como el blanco indican una correlación nula. Estos gráficos son conocidos como .Existen muchas formas de crear estos correlogramas. El siguiente enlace cubre algunas posibilidades.
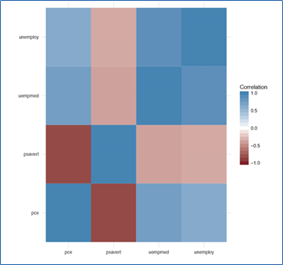
Figura 5: Diagrama calor de la correlación del dataset economics
Creación de autor: Alfonso PradoFigura 5: Diagrama calor de la correlación del dataset economics
Creación de autor: Alfonso Prado
2.1.2 Covarianza
Hemos visto que la correlación indica la relación que existe entre dos variables; es decir, si una de ellas (la variable predictora) cambia, la variable de respuesta también cambiará, ya sea hacia arriba o hacia abajo.
Por otro lado, la covarianza es un valor que indica el grado de variación conjunta de dos variables aleatorias respecto a sus medias. Es el dato básico para determinar si existe una dependencia entre ambas variables y es esencial para estimar otros parámetros fundamentales, como el coeficiente de correlación lineal o la recta de regresión. También ayuda a entender si estas dos variables están relacionadas de alguna forma.
Retorna un valor que puede ser positivo (si se mueven juntas), negativo (si se mueven en direcciones opuestas), o nulo (si no se mueven juntas de manera apreciable). Existen varios métodos (algoritmos) para su cálculo.
En otras palabras, la covarianza trata de encontrar la relación entre dos variables predictoras. Se asume que hay una variable predictora que provoca cambios entre las variables de respuesta. Queremos encontrar la relación entre estas dos variables predictoras.
La función para determinar la covarianza y su fórmula de cálculo se puede ver en la siguiente gráfica:

Figura 6: Sintaxis de la función cov (a) y su fórmula de cálculo (b)
Referencia: Sintaxis de la función, www.rdocumentation.orgFigura 6: Sintaxis de la función cov (a) y su fórmula de cálculo (b)
Referencia: Sintaxis de la función, www.rdocumentation.org
2.1.3 Correlación con variables categóricas
Hasta el momento, hemos visto cómo cuantificar la relación entre variables cuantitativas numéricas, pero, como mencionamos antes, estas no son el único tipo de variables que la estadística puede procesar. Otro caso importante es el de las variables nominales. Para este tipo de datos, utilizamos tablas de contingencia.
De acuerdo con Agresti A. (2013), el análisis de datos categóricos se basa típicamente en tablas de contingencia de dos o más dimensiones, tabulando la frecuencia de ocurrencia de niveles de datos nominales y/o ordinales. Una tabla de contingencia es una herramienta que permite organizar datos categóricos en filas y columnas, mostrando la frecuencia de ocurrencia de cada combinación de valores. Esta tabla nos permite medir la interacción entre dos variables y obtener información valiosa para comprender mejor los resultados de una investigación.
Por ejemplo, trabajando con el dataset Oncho, este dataset describe la cantidad de personas encuestadas para saber si padecen de esta enfermedad (onchocercosis). Tenemos una variable que indica si está infectada la persona, pero también contiene otras variables como el área (Savannah o Rainforest), sex (el género masculino o femenino) y grupo de edad (0-20, 20-39, 40+). Todas estas variables son tipo categórico.
En R, estas variables pueden ser convertidas al tipo factor. Un factor no es nada más que una variable categórica que permite agrupación y las distintas opciones de cada variable toman el nombre de niveles del factor. Por ejemplo, para el factor “área” hay 2 niveles: Savannah o Rainforest.
Con estos datos podemos crear una tabla de contingencia que nos permita medir la relación entre estas variables en términos de frecuencia de ocurrencia en el dataset, por ejemplo, no infectados en la Savannah tenemos 267 personas mientras que infectadas en la misma área 281.
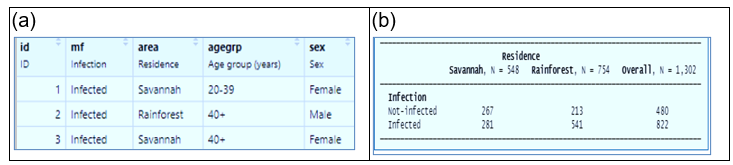
Figura 7:Dataset (a) y tabla de contingencia (b)
Figura 7:Dataset (a) y tabla de contingencia (b)

Debemos notar que la cantidad de observaciones de un nivel nominal no va a ser necesariamente la misma de otro nivel. Por ejemplo, la cantidad de encuestados hombres (Male) no es igual a las mujeres (Female).
En algunos campos de investigación como la bioestadística se estila crear la tabla con nombres genéricos como Exposure y Outcome, donde las filas (Exp+ y Exp-) indican haber estado sujeto a un “tratamiento” y las columnas conocidas como Out+ y Out- haber desarrollado un efecto o no. En nuestro dataset Oncho, el área sería el “tratamiento” y
mfel “efecto”.Los datos de frecuencia de la tabla por sí solos no indican mayor cosa, por lo tanto, la tabla debe ser procesada a fin de obtener algunos estadísticos que nos indiquen si existe una relación entre un par de variables. El proceso de análisis va a ser diferente si la tabla es de 2x2 (dos filas y dos columnas) o de más filas, como por ejemplo si analizamos la variable “agegrp”.
Para el caso de variables dicotómicas (esto es, variables que solo tienen dos posibles niveles) la función
epi.2by2()nos ayuda a obtener los estadísticos necesarios, pero para tablas más grandes la funciónchisq.test()sería la apropiada. Analizaremos estas funciones más adelante en el curso.Tratamiento de tablas de contingencia
Describe distintas funciones utilizadas en el análisis enlace -
2.2 Causación
Las medidas de correlación y covarianza nos indican cómo cambia una variable cuando la otra variable cambia. Es decir, solo nos indican cómo se mueven las variables en el dataset, pero no necesariamente nos indican que una variable causa a la otra variable.
Ejemplo: Usted dispone de un dataset que contiene población de una ciudad, el consumo de carne y el consumo de pescado en la ciudad. Existe una correlación directa entre las dos últimas variables y la población. Esto es correcto porque se asume que mientras más grande es la población de una ciudad, hay más consumo.
Pero, si se efectúa una correlación entre consumo de pescado y consumo de carne también encontrará correlación directa. ¿Significa esto que el consumo de carne hace que se consuma más pescado? Por supuesto que no. En este caso existe correlación, pero no existe causación, es decir, el consumo de carne no produce que se consuma más pescado. Por lo tanto, diremos que la causación implica correlación, pero la correlación no implica causación.
Análisis de Correlación
Describe varias funciones para análisis de correlación y causaciónAprende más
Para conocer más sobre el tema, puedes leer el siguiente artículo ¡Accede aquí!
2.2.1 Diseño de Experimentos
De acuerdo con Mendiburu F, Yaseen M. (2020), el propósito del diseño de experimentos (DoE) es poder obtener en forma segura la relación causa-efecto entre dos variables. Por ejemplo: saber si un cierto medicamento ayudó (o no) en la recuperación del paciente. Para aseverar que lo anterior es verdadero ciertas consideraciones deben cumplirse.
Asociación
El primer criterio para establecer un efecto causal es una asociación observada entre la variable predictora y de respuesta. Generalmente esto se logra mediante un análisis de correlación. Por otro lado, debemos garantizar que existe la relación tiene un ordenamiento en el tiempo. Se debe asegurar que la variación de la variable predictora se produjo antes del tiempo de la variación de la variable de respuesta.
Detección de asociaciones espurias
El segundo criterio es que esta relación no sea espuria, definimos como espuria a una relación que es ficticia o fraudulenta. Muchas veces nos topamos con la existencia de una tercera variable que en realidad afecta a las dos primeras. Este tipo de variable se las conoce como “confounding” (que produce confusión).
La siguiente figura ilustra la relación entre la edad del paciente y el riesgo de enfermedad coronaria. En principio parecería que la edad es un factor, pero la variable confounding sería el ejercicio.

Figura 8: Correlación vs Causación en enfermedad coronaria
Creación de autor: Alfonso PradoFigura 8: Correlación vs Causación en enfermedad coronaria
Creación de autor: Alfonso Prado
Para garantizar que la relación no sea espuria debemos cumplir las siguientes condiciones:
- Dos grupos de comparación (en el caso más simple, un grupo experimental y un grupo de control), para establecer asociación.
- Variación en la variable independiente se produce antes del cambio en la variable dependiente, para establecer el orden temporal.
- Asignación aleatoria a los dos (o más) grupos de comparación, para establecer que la relación no es espuria.
-
-
-
Actividades
-
Hacer un envío
-
Hacer intentos: 1
-
-
-
Resultado de aprendizaje 2
-
Ruta Académica - RDA2 - T1 TareaNo disponible hasta que: Su Dirección de correo es mariverata@puce.edu.ec
-
Ruta Académica - RDA2 - T2 TareaNo disponible hasta que: Su Dirección de correo es mariverata@puce.edu.ec
-
-
-
Enlaces de Sesiones
-
Enlaces de Grabaciones
-
Material extra
-
-
-
Bienvenidos a PUCE CAFÉ: Un Espacio Abierto para la Participación y Reflexión
PUCE CAFÉ es un espacio diseñado para fomentar la conversación abierta y el intercambio de ideas entre los participantes del aula virtual. Aquí, les invitamos a reflexionar sobre los temas abordados, plantear preguntas, y compartir inquietudes sobre los contenidos trabajados.
Este es el lugar perfecto para aclarar dudas, profundizar en conceptos y mejorar la comprensión de los temas. Pueden discutir aspectos como la incorporación de multimedia en Moodle, la organización y categorización de contenidos, y las mejores prácticas para mejorar la accesibilidad y la experiencia de usuario en entornos de aprendizaje virtual.
Recuerden, no existen preguntas incorrectas; cada aporte, ya sea una pregunta o comentario, contribuye a enriquecer la experiencia de aprendizaje colectiva. Los animamos a participar activamente, ya que, además de contar con nuestro apoyo, también pueden aprender de los conocimientos y experiencias compartidas por sus compañeros.
¡Esperamos sus preguntas y comentarios para seguir construyendo juntos este proceso de aprendizaje!
-
-
-
Descargar el contenido de la Clase 1
Descargar el contenido de la Clase 2
Descargar el contenido de la Clase 3
Descargar el contenido de la Clase 4
Descargar el contenido de la Clase 5
Descargar el contenido de la Clase 6
Descargar el contenido de la Clase 7
Descargar el contenido de la Clase 8
Descargar el contenido de la Clase 9
Descargar el contenido de la Clase 10
Descargar el contenido de la Clase 11
Descargar el contenido de la Clase 12
Descargar el contenido de la Clase 13
Descargar el contenido de la Clase 14
Descargar el contenido de la Clase 15
Descargar el contenido de la Clase 16
-
-
-
SERIES TEMPORALESConocida también como serie cronológica. Es la sucesión de observaciones cuantitativas ordenadas en el tiempo de un fenómeno. Los datos tienen un orden que no es posible variar. La información puede ser mensual, trimestral, anual o de cualquier otro intervalo temporal.VARIABLE ALEATORIAConocida también como variable estocástica o probabilística. Es la característica considerada en un experimento aleatorio cuyo valor de ocurrencia solo puede saberse con exactitud una vez observado.
-
CORRELOGRAMAEs un gráfico que permite apreciar las autocorrelaciones r₁, r₂, ..., rₖ mediante el cual se identifican si los datos de una serie de tiempo tienen las siguientes características: estacionalidad, aleatoriedad, tendencia y estacionariedad.PRUEBA CHI CUADRADODe acuerdo con Ramírez-Alan (2016), “El test Χ² considera la hipótesis nula (H₀) de que las variables son independientes. Si esto es verdad, la frecuencia de ocurrencia debería estar dada por la cantidad de casos totales multiplicada por la probabilidad esperada”.
En el ejemplo anterior, si la probabilidad de compra es igual para los 3 niveles socioeconómicos (πᵢⱼ = 33%), entonces si se han vendido 1000 ítems, estos deberían estar distribuidos en las 3 categorías (n*πᵢⱼ = 1000*0.33), valor conocido como μᵢⱼ.
Pero si Hₐ está en lo correcto, va a existir una diferencia entre la frecuencia observada (ηᵢⱼ) y la esperada (μᵢⱼ), indicando que existe algún fenómeno por detrás que influencia la frecuencia observada. La prueba Χ² calcula esta diferencia de la siguiente forma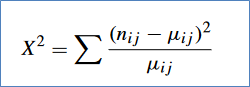
-
ProbabilidadProbabilidad significa posibilidad. Es una rama de las matemáticas que estudia la ocurrencia de un evento aleatorio. El valor se expresa de cero a uno. La probabilidad se ha introducido en las matemáticas para predecir la probabilidad de que ocurran eventos. El significado de probabilidad es básicamente el grado en el que es probable que algo suceda. Esta es la teoría básica de la probabilidad, que también se utiliza en la distribución de probabilidad, donde aprenderá la posibilidad de resultados para un experimento aleatorio. Para encontrar la probabilidad de que ocurra un solo evento, primero debemos saber el número total de resultados posibles.Probabilidad acumulativaLa probabilidad acumulada se refiere a la probabilidad de que el valor de una variable aleatoria se encuentre dentro de un rango determinado. Por ejemplo:
Pr(a ≤ X ≤ b)
Donde X es una variable aleatoria y a y b son los límites del rango. Con frecuencia, se utiliza para calcular la probabilidad de que una variable aleatoria sea menor o igual a un valor especificado:
Pr(X ≤ b)Probabilidad clásica (a-priori)La probabilidad a priori, también conocida como probabilidad clásica, es una probabilidad que se deduce del razonamiento formal. En otras palabras, la probabilidad a priori se deriva del examen lógico de un evento. La probabilidad a priori no varía de persona a persona (como lo haría una probabilidad subjetiva) y es una probabilidad objetiva.Probabilidad condicionalLas probabilidades condicionales se escriben como P(A|B), que puede leerse como "la probabilidad de que A ocurra DADO que B ha ocurrido". Si conocemos probabilidades como P(A), P(B) y P(A|B), podemos hallar otras probabilidades como P(B|A).Probabilidad totalLa regla de probabilidad total (también conocida como ley de probabilidad total) es una regla fundamental en estadística relacionada con las probabilidades condicionales y marginales. La regla establece que, si se desconoce la probabilidad de un evento, se puede calcular utilizando las probabilidades conocidas de varios eventos distintos.Teorema de BayesEl teorema de Bayes es una fórmula matemática sencilla que se utiliza para calcular probabilidades condicionales. Ocupa un lugar destacado en los enfoques subjetivistas o bayesianos de la epistemología, la estadística y la lógica inductiva. Los subjetivistas, que sostienen que la creencia racional está regida por las leyes de la probabilidad, se apoyan en gran medida en las probabilidades condicionales en sus teorías de la evidencia y sus modelos de aprendizaje empírico.
El teorema de Bayes es fundamental para estas empresas, tanto porque simplifica el cálculo de las probabilidades condicionales como porque aclara características significativas de la posición subjetivista. De hecho, la idea central del teorema —que una hipótesis se confirma por cualquier conjunto de datos que su verdad haga probable— es la piedra angular de toda la metodología subjetivista. -
Distribución NormalLlamada también como distribución de Gauss, es la distribución de probabilidad más utilizada en estadística y teoría de probabilidad. Esto se debe a dos razones:
- Su función de densidad es simétrica y con forma de campana lo que favorece su aplicación como modelo a gran número de variables.
- Es además límite de otras distribuciones y aparece relacionada con resultados ligados a la teoría de las probabilidades gracias a sus propiedades matemáticas.AsimetríaEs la falta de simetría entre los datos de una distribución. El concepto de asimetría se refiere a si la curva que forman los valores de la serie presenta la misma forma a la izquierda y derecha de un valor central (media aritmética). -
Inferencia estadísticaLa inferencia estadística es el conjunto de métodos y técnicas que permiten inducir, a partir de la información empírica proporcionada por una muestra, cuál es el comportamiento de una determinada población con un riesgo de error medible en términos de probabilidad.Intervalo de confianzaEl intervalo de confianza describe la variabilidad entre la medida obtenida en un estudio y la medida real de la población (el valor real). Corresponde a un rango de valores, cuya distribución es normal y en el cual se encuentra, con alta probabilidad, el valor real de una determinada variable. Esta «alta probabilidad» se ha establecido por consenso en 95%. Así, un intervalo de confianza de 95% nos indica que dentro del rango dado se encuentra el valor real de un parámetro con 95% de certeza.
-
Distribución BernoulliLa distribución de Bernoulli es una distribución discreta que está relacionada con muchas distribuciones, tales como la distribución binomial, geométrica y binomial negativa. La distribución de Bernoulli representa el resultado de 1 ensayo. Las secuencias de ensayos de Bernoulli independientes generan las demás distribuciones: la distribución binomial modela el número de éxitos en n ensayos, la distribución geométrica modela el número de fallas antes del primer éxito y la distribución binomial negativa modela el número de fallas antes del éxito xésimo.EnsayosPiense en los ensayos como repeticiones de un experimento. La letra n denota el número de ensayos. Solo hay dos resultados posibles, llamados "éxito" y "fracaso", para cada ensayo. La letra p denota la probabilidad de éxito en un ensayo y q denota la probabilidad de fracaso en un ensayo, cumpliéndose que: p + q = 1.
-
PMFUna función de probabilidad o función de masa de probabilidad es una función que devuelve la probabilidad de que una variable aleatoria discreta sea exactamente igual a algún valor. Es una función que asocia a cada punto de su espacio muestral X la probabilidad de que esta lo asuma.Proceso de PoissonSea X(t) el número de ocurrencias del evento con el tiempo (el proceso); entonces X(t) consiste en funciones de valores enteros no-decrecientes. La probabilidad de que sucedan exactamente k eventos en el tiempo t es:
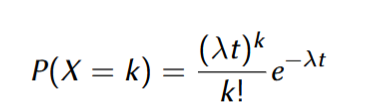
-
Re-muestreoLas técnicas de remuestreo son métodos para crear nuevas muestras de datos a partir de un conjunto de datos existente mediante el uso de selección aleatoria o manipulación. La idea es imitar el proceso de muestreo de la población de interés, sin hacer suposiciones sobre su distribución o parámetros.Grados de LibertadEn la estadística inferencial, el término grados de libertad se define normalmente como el número de observaciones que son libres de variar, dada una o más restricciones matemáticas, en un conjunto de valores utilizados para estimar alguna característica de la población.
Dicho de otra manera, los grados de libertad son el número de observaciones independientes menos el número de restricciones asociado a esas observaciones. -
ERRORES TIPO I Y TIPO IIEn la teoría de decisiones, es el error TIPO I es el que se comete al rechazar la hipótesis nula H 0, cuando es verdadera.
El error tipo II, es el error que se comete al aceptar la hipótesis nula H 0 cuando es falsa. REGIÓN DE ACEPTACIÓN y RECHAZOEs la región formada por el conjunto de valores con los cuales decidimos aceptar la hipótesis nula, el área de rechazo conocida también como región crítica, está formada por el conjunto de valores con los cuales se rechaza la hipótesis nula.
REGIÓN DE ACEPTACIÓN y RECHAZOEs la región formada por el conjunto de valores con los cuales decidimos aceptar la hipótesis nula, el área de rechazo conocida también como región crítica, está formada por el conjunto de valores con los cuales se rechaza la hipótesis nula. -
Distribución gammaLa distribución de gamma es una distribución de probabilidad continua que se utiliza para modelar el tiempo de espera hasta que ocurran un número específico de eventos. Es una distribución de dos parámetros, lo que significa que se requiere dos parámetros para definir completamente la distribución. Los dos parámetros son el parámetro de forma, denotado por alfa (α) y el parámetro de escala, denotado por beta (β).El parámetro de forma controla la forma de la distribución, mientras que el parámetro de escala controla la propagación de la distribución.Factores y nivelesUn factor es una variable categórica con un número finito de valores o niveles. En R, los factores se utilizan habitualmente para realizar clasificaciones de los datos, estableciendo su pertenencia a los grupos o categorías determinados por los niveles del factor.
Los niveles de un factor pueden estar codificados como valores numéricos o como caracteres. Independientemente del tipo, internamente R almacena los factores como números enteros, lo cual permite optimizar el uso de memoria. -
INTERVALO DE CONFIANZAConocido también como límites de confianza. Es un rango de valores en el cual se encontraría el valor del parámetro, con una probabilidad determinada.
Generalmente se construye intervalos de confianza con 95% de probabilidadANALISIS DE RESIDUOSEn el contexto de la regresión lineal, llamamos residuos a las diferencias entre los valores de la variable dependiente observados y los valores que predecimos a partir de nuestra recta de regresión. -
COEFICIENTE DE DETERMINACIÓN AJUSTADO r^2El R cuadrado ajustado es una versión modificada del R cuadrado que tiene en cuenta los predictores que no son significativos en un modelo de regresión. En otras palabras, el R cuadrado ajustado muestra si la adición de predictores adicionales mejora o no un modelo de regresión. El coeficiente de determinación mide la proximidad del ajuste de la ecuación de regresión de la muestra a los valores observados de la variable dependiente.DIAGRAMA DE CAJASConocido también como BOXPLOT. Es un importante gráfico del análisis exploratorio de datos. Al igual que el histograma, permite tener una idea visual de la distribución de los datos. Permite determinar si hay simetría, ver el grado de variabilidad existente y detectar los "outliers" (datos muy diferentes al conjunto de información), es decir la existencia de posibles datos discordantes. Además, el Boxplot es bien útil para comparar grupos. Es un diagrama que muestra la distancia en que se encuentran los datos y cómo están distribuidos equitativamente.
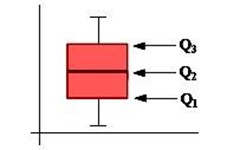 SUMA DE CUADRADOS DE RESIDUOSLa suma de cuadrados residuales , también conocida como la suma de los residuos al cuadrado o la suma de la estimación al cuadrado de los errores , es la suma de los cuadrados de los residuos (desviaciones predichas de los valores empíricos reales de los datos) . Es una medida de la discrepancia entre los datos y un modelo de estimación. Un pequeño SSRes indica un ajuste ajustado del modelo a los datos. Se utiliza como criterio de optimización en la selección de parámetros y la selección de modelos.
SUMA DE CUADRADOS DE RESIDUOSLa suma de cuadrados residuales , también conocida como la suma de los residuos al cuadrado o la suma de la estimación al cuadrado de los errores , es la suma de los cuadrados de los residuos (desviaciones predichas de los valores empíricos reales de los datos) . Es una medida de la discrepancia entre los datos y un modelo de estimación. Un pequeño SSRes indica un ajuste ajustado del modelo a los datos. Se utiliza como criterio de optimización en la selección de parámetros y la selección de modelos.
En el contexto de ANOVA este estadístico se llama SST
Dado por la fórmula siguiente: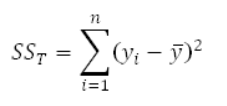
-
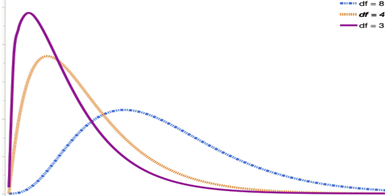
Distribución Chi-cuadradoLa distribución ji cuadrado es una familia de distribuciones. Cada distribución se define por los grados de libertad. (Los grados de libertad se comentan en mayor detalle en las páginas sobre la prueba de bondad de ajuste y la prueba de independencia). En la siguiente figura se muestran tres distribuciones ji cuadrado diferentes, con distintos grados de libertad.
 Prueba de Chi cuadradoLa prueba Chi-cuadrado es una prueba de hipótesis utilizada para determinar si existe una relación entre dos variables categóricas. La prueba Chi-cuadrado comprueba si las frecuencias que se dan en la muestra difieren significativamente de las frecuencias que cabría esperar. Así, se comparan las frecuencias observadas con las esperadas y se examinan sus desviaciones.
Prueba de Chi cuadradoLa prueba Chi-cuadrado es una prueba de hipótesis utilizada para determinar si existe una relación entre dos variables categóricas. La prueba Chi-cuadrado comprueba si las frecuencias que se dan en la muestra difieren significativamente de las frecuencias que cabría esperar. Así, se comparan las frecuencias observadas con las esperadas y se examinan sus desviaciones. -
Odds y log OddsLas probabilidades (técnicamente, las probabilidades de éxito) se definen como la probabilidad de éxito/probabilidad de fracaso. Por lo tanto, la probabilidad de éxito (80 % de probabilidad de lluvia) tiene una probabilidad de fracaso (20 % de probabilidad de que no llueva); como ecuación (la "razón de probabilidades"), es 0,8/0,2 = 4. El logaritmo de las probabilidades es el logaritmo de las probabilidades. ln(4) = 1,38629436 ≅ 1,386.ImputaciónLa imputación de datos es una técnica estadística que se utiliza para reemplazar valores faltantes o nulos en un conjunto de datos. En el análisis de datos y la ciencia de datos, el manejo de los datos faltantes es crucial, ya que pueden afectar significativamente los resultados de cualquier análisis. La imputación de datos tiene como objetivo proporcionar un conjunto de datos más completo, lo que permite un modelado y un análisis más precisos. Existen varios métodos para la imputación de datos, cada uno con sus fortalezas y debilidades, según la naturaleza de los datos y el contexto del análisis.
La imputación de media, mediana y moda se encuentran entre las formas más simples de imputación de datos. La imputación de media reemplaza los valores faltantes con el promedio de los datos disponibles, mientras que la imputación de mediana utiliza el valor medio; y la imputación de moda utiliza el valor que aparece con mayor frecuencia. Estos métodos son fáciles de implementar y comprender, pero pueden introducir sesgos, especialmente en distribuciones sesgadas. -
Varianza insesgadaUn estimador insesgado de la varianza es aquel cuya distribución de estimaciones, al tomar múltiples muestras, tiene una media que es igual a la varianza poblacional real.
La insesgabilidad es una propiedad deseable en los estimadores, ya que garantiza que, en promedio, el estimador no se desvía sistemáticamente del valor verdadero del parámetro que se está estimandoLikelihoodEn estadística, la función de verosimilitud (o simplemente, verosimilitud) es una función que permite realizar inferencias sobre los parámetros de un modelo estadístico, basándose en un conjunto de observaciones.
Función de Verosimilitud:
Es una función que evalúa qué tan bien un modelo estadístico describe los datos observados, para un determinado conjunto de parámetros. -
Distribución chi-cuadrado¿Qué es una distribución chi-cuadrado?
Las distribuciones chi-cuadrado (Χ2) son una familia de distribuciones de probabilidad continuas. Se utilizan ampliamente en pruebas de hipótesis, incluyendo la prueba de bondad de ajuste chi-cuadrado y la prueba de independencia chi-cuadrado.
La forma de una distribución chi-cuadrado está determinada por el parámetro k, que representa los grados de libertad.
Muy pocas observaciones del mundo real siguen una distribución chi-cuadrado. El objetivo principal de las distribuciones chi-cuadrado es comprobar hipótesis, no describir distribuciones del mundo real.
Estadísticos de la prueba chi-cuadrado
Las pruebas chi-cuadrado son pruebas de hipótesis con estadísticos de prueba que siguen una distribución chi-cuadrado bajo la hipótesis nula. La prueba chi-cuadrado de Pearson fue la primera prueba chi-cuadrado que se descubrió y es la más utilizada.Cp de MallowsEs un estimador que ayuda a alcanzar un equilibrio importante con el número de predictores en el modelo. El Cp de Mallows compara la precisión y el sesgo del modelo completo con modelos que incluyen un subconjunto de los predictores.
Generalmente, debe buscar modelos en los que el valor de Cp de Mallows sea pequeño y esté cercano al número de predictores en el modelo más la constante (p). Un valor de Cp pequeño indica que el modelo es relativamente preciso (tiene una varianza pequeña) para estimar los coeficientes de regresión verdaderos y pronosticar futuras respuestas. Un valor del Cp de Mallows que se aproxima al número de predictores más la constante indica que el modelo relativamente no tiene sesgo en la estimación de los verdaderos coeficientes de regresión y el pronóstico de respuestas futuras. Modelos con falta de ajuste y sesgo poseen valores de Cp de Mallows más grandes que p.
-
-
-
- Bruce, P. (Il.), Bruce, A. & Gedeck, P. (2022). Estadística práctica para ciencia de datos con R y Python: (2 ed.). Marcombo. https://elibro.puce.elogim.com/es/ereader/puce/281858?page=1
- Miller I , Freund J, (2006) Estadistica para ingenieros, McGraw Hiil https://catalogobiblioteca.puce.edu.ec/cgi-bin/koha/opac-detail.pl?biblionumber=18693
- Martinez M. ( 2020) Bioestadistica Amigable, Elsevier https://catalogobiblioteca.puce.edu.ec/cgi-bin/koha/opac-detail.pl?biblionumber=286887
-
- Gutiérrez A. (2007). Estadística General Aplicada. Universidad EAFIT.
- López W. (2020). Estadística Práctica: Aplicación y análisis para la toma de decisiones. Publicado Independientemente.
-
- Webster A. (2000). Estadística aplicada a los negocios. Irwin Professional Publishing.
- Agresti A. (2013). Categorical Data Analysis. John Wiley & Sons Publication.
- Mendiburu F., Yaseen M. (2020). Experimental Designs with agricolae. Recuperado de: https://myaseen208.com/agricolae/articles/ExperimentalDesign.html
-
- Economipedia. Población estadística: Qué es, tipos y ejemplos. Recuperado de: https://economipedia.com/definiciones
- Webster A. (2000). Estadística aplicada a los negocios. Irwin Professional Publishing.
- Wasserman, L. (2010). All Statistics: A Concise Course in Statistical Inference. Springer Publishing Company.
- Otzen T., Manterola C. (2017). Técnicas de Muestreo sobre una Población a Estudio. Int. J. Morphol. vol.35 no.1 Temuco. Recuperado de: http://dx.doi.org/10.4067/S0717-95022017000100037
- Alvarez H. Conceptos de estadística. Universidad Santiago de Compostela. Recuperado de: https://www.usc.gal/genp/docencia/ConceptosDeEstadistica.pdf
-
- Economipedia. Población estadística: Qué es, tipos y ejemplos. Recuperado de: https://economipedia.com/definiciones
- Webster A. (2000). Estadística aplicada a los negocios. Irwin Professional Publishing.
- Wasserman, L. (2010). All of Statistics: A Concise Course in Statistical Inference. Springer Publishing Company.
- Otzen T., Manterola C. (2017). Técnicas de Muestreo sobre una Población a Estudio. Int. J. Morphol. vol.35 no.1 Temuco. Recuperado de: http://dx.doi.org/10.4067/S0717-95022017000100037
- Alvarez H. Conceptos de estadística. Universidad Santiago de Compostela. Recuperado de: https://www.usc.gal/genp/docencia/ConceptosDeEstadistica.pdf
-
- Webster A. (2000). Estadística aplicada a los negocios. Irwin Professional Publishing.
-
Rumsey D. (2009). Statistics II. Wiley Publishing Inc.
stats package - RDocumentation. (n.d.). Recuperado de: https://www.rdocumentation.org/packages/stats/versions/3.6.2
-
- Webster A. (2000). Estadística aplicada a los negocios. Irwin Professional Publishing.
-
- Webster A. (2000). Estadística aplicada a los negocios. Irwin Professional Publishing.
- Donnelly R. (2019). Business Statistics. Pearson Publishing.
-
- Webster A., (2000), Estadística aplicada a los negocios, Irwin Professional Publishing.
- Donnelly R. (2019). Business Statistics. Pearson Publishing. (http://www.ub.edu/) | https://dle.rae.es/inferencia
-
- Schmuller J.(2022), Statistical Analysis with Excel For Dummies, Wiley Teck K, (2022), Practical t-test Power Analysis with R, Practical Assessment, Research & Evaluation, Volumen 27, No 18 .
-
- Berman H.G., "F Distribution , descargado de https://stattrek.com/probability-distributions/f-distribution
- Rodrigo J. (2017) , ANOVA análisis de varianza para comparar múltiples medias, descargado de https://cienciadedatos.net/documentos/19_anova
-
- Webster A., (2000), Estadística aplicada a los negocios, Irwin Professional Publishing
- Bruce A. et al., (2017) Practical Statistics for Data Scientists: 50+ Essential Concepts Using R and Python, O'Reilly Media, Inc.
-
- Webster A., (2000), Estadística aplicada a los negocios, Irwin Professional Publishing
- Szretter, M. (2017), Apunte de Regresión Lineal, Universidad de Buenos Aires .
- Bruce A. et al., (2017) Practical Statistics for Data Scientists: 50+ Essential Concepts Using R and Python, O'Reilly Media, Inc.
-
- Szretter M. (2017) Apunte de Regresión Lineal, https://mate.dm.uba.ar/~meszre/apunte_regresion_lineal_szretter.pdf
- Rocha A.,(2020) Codificación de variables categóricas en aprendizaje automático, Universidad de Sevilla
- Ramirez-Alan O,(2016), Chi-Cuadrado https://rpubs.com/osoramirez/111403
- Mehdi Koosha, A. Amiri, (2019) The Effect of Link Function on the Monitoring of Logistic Regression Profiles, https://www.semanticscholar.org/
-
- Szretter M. (2017) Apunte de Regresión Lineal, https://mate.dm.uba.ar/~meszre/apunte_regresion_lineal_szretter.pdf
- Faraway J. (2020), Extending the linear model with R, CRC Press
-
- Szretter M. (2017) Apunte de Regresión Lineal, https://mate.dm.uba.ar/~meszre/apunte_regresion_lineal_szretter.pdf
- Faraway J. (2020), Extending the linear model with R, CRC Press
-
-
-
Video
-
-
Video
-
-
Idealización y Ejecución
Coordinación del Proyecto:
Javier CarreraCoordinación Administrativa:
Ana María PeñaCoordinación de Producción:
Fernando SpirituGenerador de contenido académicoAlfonso Prado
ProducciónDiseño Multimedia
- Irvin Villavicencio
- Hans Yépez
Diseño Instruccional
- Salomé Palacios
- Christian Ñacato
Tecnología de la Información
- Juan Andrade
- Carlos Guamán
Soporte y ExperienciaSoporte en aulas
- Alex Tomarema
- Adrián Yépez
Acompañamiento
- Gabriela Yánez
Experiencia de usuario
- Katherine Ramos
Marketing y FinanzasFinanciero
- María José Maldonado
Marketing
- Camila Flor
-