-
Introducción
E
n la presente clase, se explorarán los diferentes tipos de funciones de producción, la distinción entre el corto y largo plazo, y los conceptos de producto marginal, así como las leyes del producto marginal creciente y decreciente. Además, se incluirán ejemplos detallados para ilustrar estos conceptos.
Se espera que, con estas nociones, el estudiantado comience a adquirir sus habilidades en cuanto a distinguir la teoría de la producción y los costos, en la toma de decisiones de las empresas, y comprender los niveles de competencia de mercado en la economía.
Rendimientos crecientes a escala
Ocurren cuando un aumento proporcional en todos los insumos productivos genera un incremento más que proporcional en la producción. Es decir, si se duplican los factores de producción (trabajo, capital, etc.), la producción aumenta en más del doble. Esto suele darse cuando hay economías de escala, mejoras tecnológicas o mayor eficiencia en la organización del trabajo.
Rendimientos decrecientes a escala
Ocurren cuando un aumento proporcional en todos los insumos productivos genera un incremento menor que proporcional en la producción. Es decir, si se duplican los factores de producción, la producción crece en menos del doble. Esto puede ocurrir debido a problemas de coordinación, limitaciones en la infraestructura o saturación de los recursos productivos.
-
11.1. Función de producción
El análisis de una empresa o firma en la teoría microeconómica es fundamental para comprender cómo toman decisiones estos agentes económicos sobre producción, costos y maximización de beneficios. En términos generales, el estudio de la firmas explora el conjunto de decisiones relacionados a determinar la mejor combinación de factores productivos que permiten lograr producción eficiente y rentable. Esto se hace a través de diversos modelos y herramientas analíticas, que facilitan la toma de decisiones informadas que impactan en su sostenibilidad y competitividad en el mercado.
De forma ejemplar, a través de un caso en el sector automotriz, se puede ahondar en el concepto de decisión de producción, donde la empresa automotriz Toyota, dada la intensidad de competencia en su mercado, debe analizar constantemente sus decisiones de producción para encontrar el equilibrio óptimo entre insumos como trabajo, capital y tecnología. En este caso, Toyota puede implementar un Sistema de Producción Justo a Tiempo (JIT), que reduce los inventarios y optimiza la cadena de suministro. Esta estrategia se basa en la teoría de la producción eficiente, donde cada insumo se usa de la mejor manera posible para reducir desperdicios y minimizar costos de producción.
Otro ejemplo relevante para entender el fin de la teoría de la firma subyace en la industria de software, donde empresas como Microsoft y Google optimizan su producción mediante la contratación de desarrolladores altamente calificados y el uso de servidores escalables en la nube. En este sentido, el análisis detallado de las firmas les permite determinar cuántos ingenieros contratar y cuánto invertir en infraestructura digital para maximizar la producción de software sin incurrir en costos innecesarios. De manera análoga, en el sector agrícola, un productor que cultiva trigo debe decidir la cantidad de tierra, fertilizante y mano de obra que empleará para obtener el máximo rendimiento. En este caso, puede evaluar cuántos insumos adicionales le generan un beneficio adicional , evaluando eventualmente el punto a partir del cual cada unidad extra de insumo aporta menos a la producción total.
Asimismo, las empresas de energía eléctrica deben analizar su producción para determinar la combinación más eficiente entre las fuentes de energía disponibles, tanto renovables como no renovables. Por ejemplo, una empresa que decide invertir en paneles solares necesita calcular cuántos paneles instalar y cómo estos impactarán sus costos y su capacidad de generación de energía a largo plazo.
En este punto, surge el concepto de función de producción, que describe la relación entre la cantidad de insumos utilizados en la producción y la cantidad de producto obtenido. En términos más sencillos, la función de producción muestra cómo una empresa transforma factores productivos, como trabajo y capital, en bienes y servicios. Esta función es crucial para comprender la eficiencia de la producción y la toma de decisiones empresariales.
La función de producción se expresa matemáticamente de la siguiente manera:
Q = f (L, K, T)
Donde:
Q = Cantidad de producción
L = Trabajo
K = Capital
T = Tecnología
Esta ecuación indica que la producción depende de la cantidad de trabajo, capital y tecnología empleada en el proceso productivo. Cada factor productivo tiene una contribución específica a la producción total.
11.1.1. Características de la Función de Producción
Dado el carácter fundamental de la función de producción, comprender sus características resulta esencial para optimizar el uso de los recursos y mejorar la eficiencia en la producción. En este contexto, se identifican tres aspectos clave que destacan en su análisis: la relación entre insumos y producto, la eficiencia productiva y los rendimientos a escala. Estos elementos permiten evaluar cómo la combinación de factores productivos influye en la capacidad de producción, la competitividad de las empresas y la sostenibilidad de los procesos productivos en distintos sectores económicos.
Relación entre insumos y producto: Describe cómo los factores de producción, como el trabajo, el capital, la tecnología y los recursos naturales, se combinan para generar un bien o servicio. Cada insumo cumple una función específica dentro del proceso productivo y su correcta combinación determina la eficiencia y productividad de la empresa. Por ejemplo, en una fábrica de automóviles, la maquinaria y los trabajadores deben coordinarse adecuadamente para ensamblar los vehículos de manera eficiente. Asimismo, la disponibilidad y calidad de los insumos pueden influir en la cantidad y calidad del producto final, afectando la competitividad y rentabilidad de la empresa. De forma visual, se puede apreciar en la siguiente figura:
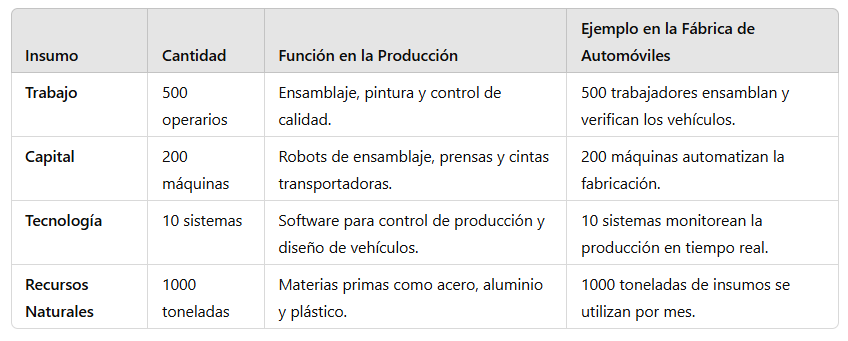
Gráfico 1: Relación entre insumo y producto - Elaboración: Docente contenidista, 2025. Gráfico 1: Relación entre insumo y producto - Elaboración: Docente contenidista, 2025.

Eficiencia productiva: Determina la cantidad máxima de bienes o servicios que una empresa puede producir utilizando de manera óptima los insumos disponibles, como trabajo, capital y recursos naturales, sin desperdiciar materiales ni tiempo. Una empresa alcanza la eficiencia productiva cuando no es posible incrementar la producción de un bien sin reducir la de otro, maximizando así el uso de sus recursos. Por ejemplo, en una fábrica de zapatos, si cada máquina y trabajador se utiliza de la mejor manera posible, se logrará la máxima producción sin aumentar costos innecesarios, lo que permite ofrecer productos competitivos en el mercado.
Rendimientos a escala: Explica cómo varía la producción cuando se incrementan todos los factores productivos en proporción. A continuación, se plantea la distinción del presente concepto para efectos del análisis de los tipos de función de producción.
Aprende más
Para conocer más sobre un estudio empírico de rendimientos a escala en el mercado farmacéutico, puedes leer el siguiente artículo ¡Accede aquí!
-
11.1.2. Tipos de Funciones de Producción
Existen tres tipos principales de retornos a escala: crecientes, constantes y decrecientes. En concreto, si al duplicar los insumos, la producción crece aún más, se dice que la función de producción presenta , lo que suele ocurrir cuando la especialización y la tecnología mejoran la eficiencia. Si la producción aumenta en la misma proporción que los insumos, se trata de una función con rendimiento constantes. Por otro lado, si el incremento en la producción es menor que el de los insumos, se presenta una función de producción con retornos decrecientes, lo cual indica ineficiencias en el proceso productivo. Una explicación más precisa se presenta a continuación.
11.1.2.1. Función de Producción de Rendimientos Constantes a Escala
En esta función de producción, un aumento proporcional en todos los insumos empleados genera un incremento en la producción en la misma proporción. Esto significa que si todos los factores productivos, como el trabajo y el capital, se duplican, la cantidad de bienes producidos también se duplica.
Matemáticamente, esta relación se expresa como:
f (2L, 2K) = 2Q
Donde:
L representa el trabajo empleado,
K el capital utilizado,
Q la cantidad de producción obtenida.
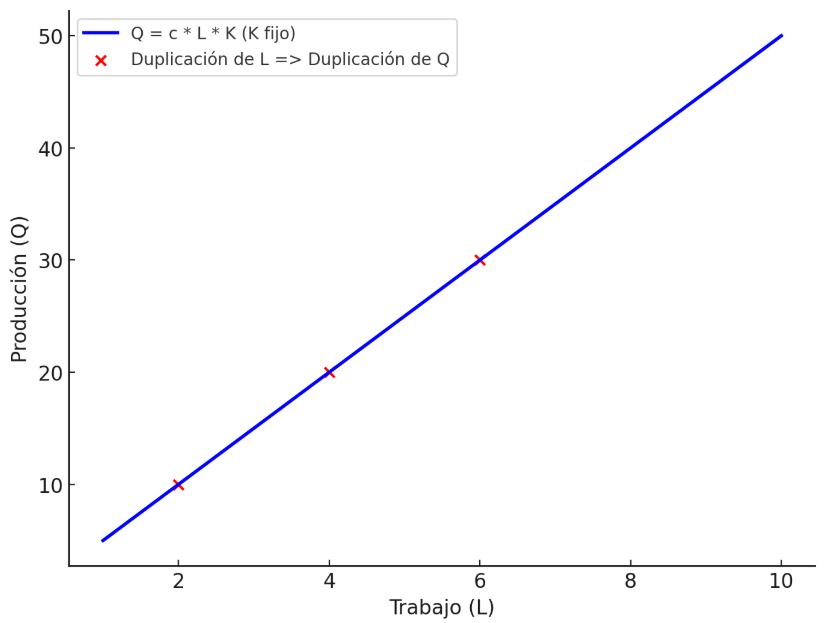
Gráfico 2: Función de producción con rendimientos constantes - Elaboración: Docente contenidista, 2025. Gráfico 2: Función de producción con rendimientos constantes - Elaboración: Docente contenidista, 2025.

Un ejemplo claro de una situación con rendimientos constantes a escala se observa en una fábrica de ensamblaje de automóviles. Si la empresa decide aumentar en un 100% tanto la cantidad de trabajadores como el número de máquinas utilizadas en el proceso de producción, se espera que la producción total de vehículos también se duplique. Esto ocurre porque cada trabajador adicional posee la maquinaria necesaria para mantener la misma eficiencia en la producción, sin generar cuellos de botella ni desperdicios en el proceso productivo.
11.1.2.2. Función de Producción de Rendimientos Crecientes a Escala
En este tipo de función de producción, un aumento proporcional en todos los factores productivos genera un incremento más que proporcional en la cantidad de bienes o servicios producidos. Es decir, si los insumos utilizados en el proceso productivo, como el trabajo y el capital, se duplican, la producción final aumenta en una proporción aún mayor.
Matemáticamente, esta relación se expresa como:
f (2L, 2K) > 2Q
Donde:
L representa la cantidad de trabajo empleado,
K el capital utilizado,
Q la producción obtenida.
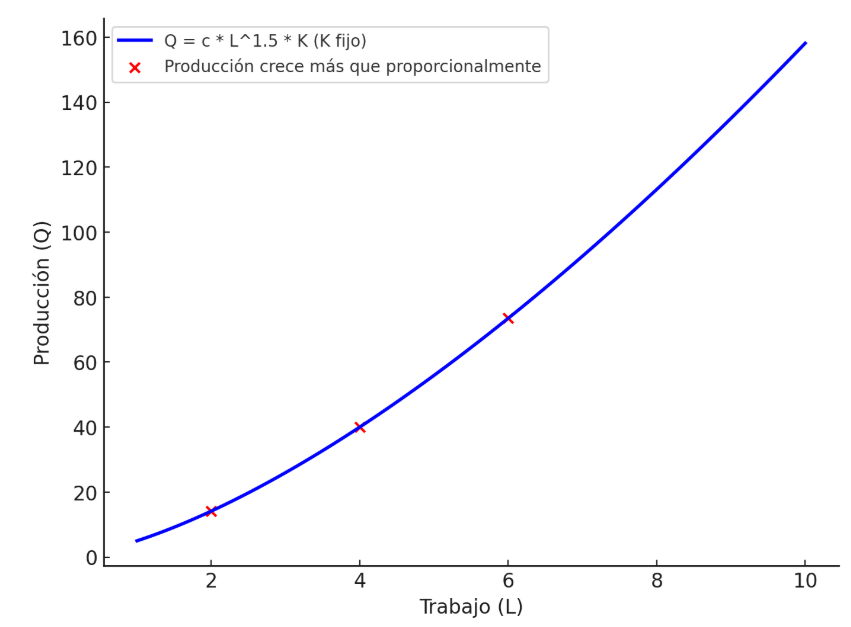
Gráfico 3: Función de producción con rendimientos crecientes - Elaboración: Docente contenidista, 2025. Gráfico 3: Función de producción con rendimientos crecientes - Elaboración: Docente contenidista, 2025.

Este fenómeno ocurre cuando los factores de producción interactúan de manera eficiente y generan sinergias que potencian la productividad total. Un claro ejemplo de ello se encuentra en el sector tecnológico, específicamente en una empresa de desarrollo de software. Si la empresa decide contratar más programadores y, al mismo tiempo, invierte en mejores servidores y herramientas de desarrollo, la producción de software no solo aumentará en proporción al incremento de insumos, sino que crecerá a un ritmo mayor.
Esto sucede porque los nuevos programadores pueden colaborar y especializarse en diferentes áreas del desarrollo, optimizando los tiempos de programación y reduciendo errores. A su vez, los servidores de mayor capacidad permiten manejar una mayor cantidad de procesos simultáneos, reduciendo los tiempos de ejecución y aumentando la eficiencia. Como resultado, la empresa experimenta un crecimiento exponencial en la cantidad de software producido, logrando mayores beneficios sin que el aumento en costos sea lineal con la producción obtenida.
11.1.2.3. Función de Producción de Rendimientos Decrecientes a Escala
En este tipo de función de producción, cuando se incrementan los insumos en una proporción determinada, el aumento en la producción resultante es menor que dicho incremento. Es decir, si los factores productivos, como el trabajo y el capital, se duplican, la cantidad de bienes o servicios producidos crece en una proporción menor.
Matemáticamente, esta relación se expresa como:
f (2L, 2K) < 2Q
Donde:
L representa la cantidad de trabajo empleado,
K el capital utilizado,
Q la producción obtenida.
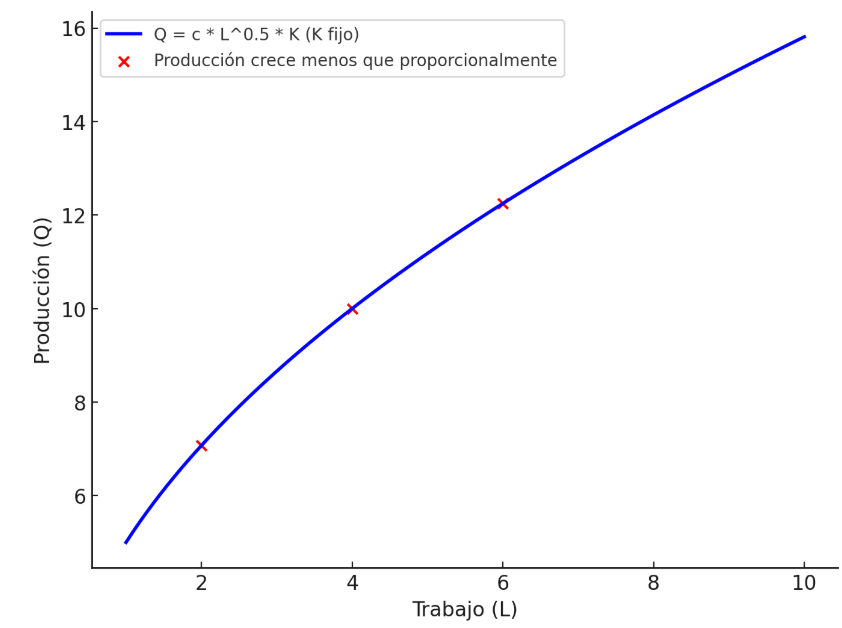
Gráfico 4: Función de producción con rendimientos decrecientes - Elaboración: Docente contenidista, 2025. Gráfico 4: Función de producción con rendimientos decrecientes - Elaboración: Docente contenidista, 2025.

Este fenómeno ocurre cuando existen restricciones o limitaciones en la producción que impiden que los insumos adicionales sean aprovechados de manera eficiente. Estas restricciones pueden deberse a factores físicos, tecnológicos o de organización.
Un claro ejemplo de esta situación se observa en una pequeña granja con espacio de cultivo limitado. Si el dueño decide duplicar la cantidad de trabajadores y maquinaria con la intención de aumentar la producción de alimentos, podría enfrentarse a un problema de eficiencia. Aunque haya más personas trabajando y más herramientas disponibles, la superficie de tierra cultivable sigue siendo la misma. Esto significa que los nuevos trabajadores deberán compartir el mismo espacio y los mismos recursos, lo que puede generar congestión y reducir la productividad individual.
En consecuencia, la producción total de la granja aumentará, pero en menor proporción al incremento de insumos. En lugar de duplicarse, el crecimiento será más reducido, debido a la saturación de los recursos disponibles. Esta situación refleja los , donde los factores productivos adicionales generan beneficios cada vez menores a medida que se utilizan en un entorno con restricciones.
-
11.1.3. Producción en el Corto y Largo Plazo
En el análisis económico de la producción, es fundamental distinguir entre el corto y el largo plazo, ya que cada uno presenta diferentes restricciones y posibilidades para las empresas. La diferencia entre ambos radica en la flexibilidad que tienen las firmas para ajustar sus factores productivos en respuesta a cambios en la demanda o en las condiciones del mercado.
A continuación, se explorarán en detalle estas dos perspectivas y sus implicaciones en la toma de decisiones empresariales.
11.1.3.1. Corto Plazo
El corto plazo es el período en el que al menos un factor de producción es fijo. Normalmente, el capital (maquinaria, instalaciones) se considera fijo, mientras que el trabajo es variable. Por ejemplo, una panadería puede contratar más empleados para aumentar la producción de pan, pero en el corto plazo no puede expandir su local ni comprar nuevas máquinas de horneado.

Gráfico 5: Ilustración de la producción panadera en corto plazo Gráfico 5: Ilustración de la producción panadera en corto plazo

11.1.3.2. Largo Plazo
En el largo plazo, todos los factores de producción son variables. Esto permite a las empresas ajustar completamente su capacidad productiva y responder mejor a cambios en la demanda del mercado. En este caso, una empresa de tecnología puede decidir construir una nueva sede, comprar equipos de última generación y contratar más empleados, ajustando todos los insumos a sus necesidades de producción.
-
11.1.4. Producto Marginal y sus variaciones
Toda vez que se ha comprendido el concepto de retornos de escala, en el análisis de la producción, el concepto de producto marginal es fundamental para comprender cómo varía la producción total cuando se incrementa la cantidad de un insumo, manteniendo constantes los demás factores. El producto marginal permite a las empresas evaluar la eficiencia de cada unidad adicional de insumo y tomar decisiones estratégicas sobre la asignación de recursos. Dependiendo de la etapa de producción en la que se encuentre una empresa, este producto marginal puede ser creciente o decreciente.
El producto marginal mide el cambio en la producción total cuando se incrementa un insumo, manteniendo las demás constantes.
Matemáticamente:
PMgL = ΔQ / ΔL
Donde PMgL es el producto marginal del trabajo.
A continuación, se explican estas dos situaciones con ejemplos que ilustran su impacto en la productividad y eficiencia empresarial.
11.1.4.1. Producto Marginal Creciente
Ocurre cuando agregar más unidades de un insumo genera incrementos progresivos en la producción total. Por ejemplo, en una fábrica, los primeros trabajadores adicionales pueden aumentar la eficiencia al dividir tareas, lo que eleva la producción en una proporción mayor al incremento del trabajo, como se puede observar a continuación:
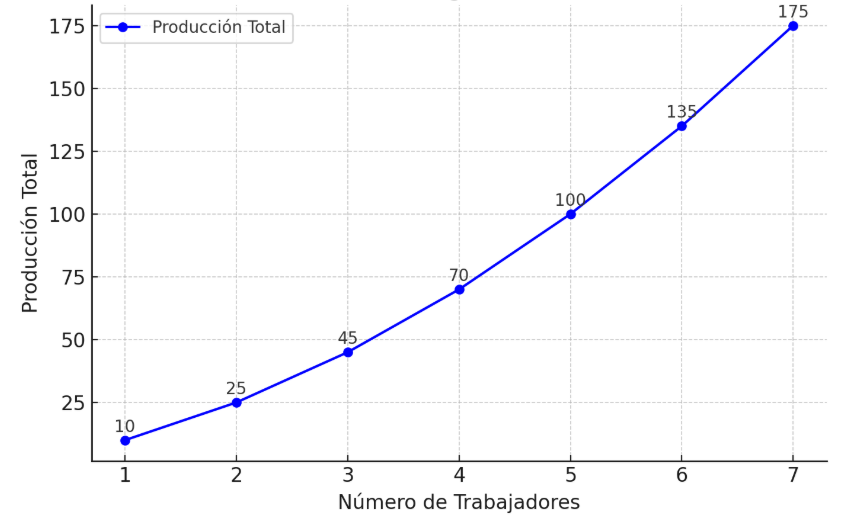
Gráfico 6: Producción marginal creciente en trabajo - Elaboración: Docente contenidista, 2025. Gráfico 6: Producción marginal creciente en trabajo - Elaboración: Docente contenidista, 2025.

11.1.4.2. Producto Marginal Decreciente
Sucede cuando agregar más unidades de un insumo produce aumentos cada vez menores en la producción total. En este caso, dentro de una oficina, añadir más empleados sin aumentar el espacio o los recursos puede reducir la productividad por hacinamiento y falta de equipos.
Aprende más
Para conocer más sobre un estudio empírico de rendimientos decrecientes, puedes leer el siguiente artículo ¡Accede aquí!
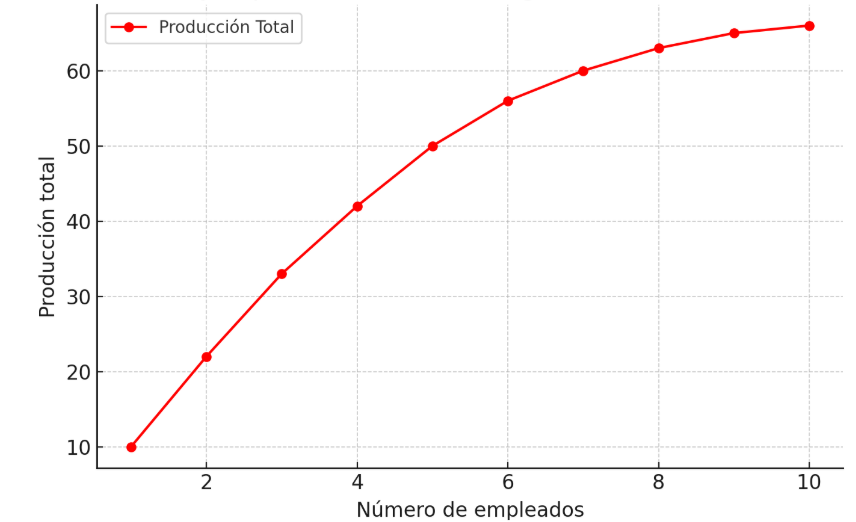
Gráfico 7: Producción marginal decreciente en trabajo - Elaboración: Docente contenidista, 2025. Gráfico 7: Producción marginal decreciente en trabajo - Elaboración: Docente contenidista, 2025.

La función de producción es un pilar en la economía, ya que permite entender la relación entre insumos y bienes producidos. Los diferentes tipos de funciones de producción explican cómo varía la producción ante cambios en los factores productivos. Por otra parte, la distinción entre corto y largo plazo permite comprender las restricciones y decisiones estratégicas de las empresas. Finalmente, el análisis del producto marginal ayuda a determinar el nivel óptimo de uso de los recursos y mejorar la eficiencia productiva en diversos sectores.
Profundiza más
Este recurso te ayudará a enfatizar sobre como la función de producción es fundamental para entender cómo las empresas transforman insumos en productos finales ¡Accede aquí!
-
-
-
Actividades