-
Sistemas numericos
Sistema Decimal Sistema Binario Valor Notación Nombre Valor Notación Nombre 1 B byte 1 byte byte 1000 kB kilobyte 10241 KiB kibibyte 10002 MB megabyte 10242 MiB mebibyte 10003 GB gigabyte 10243 GiB gibibyte 10004 TB terabyte 10244 TiB tebibyte 10005 PB petabyte 10245 PiB pebibyte 10006 EB exabyte 10246 EiB exbibyte 10007 ZB zettabyte 10247 ZiB zebibyte 10008 YB yottabyte 10248 YiB yobibyte 10009 RB ronnabyte 10249 - - 100010 QB quettabyte 102410 - - Tabla 1: Magnitudes de datos Unidad Equivalente Aproximado 1 bit Una variable booleana que indica verdadero (1) o falso (0). 1 byte Un carácter latino básico. 1 kilobyte Texto de "Jabberwocky"
Un típico favicon1 megabyte Texto de Harry Potter y el cáliz de fuego 1 gigabyte Aproximadamente media hora de video
Audio sin comprimir con calidad de CD de "The Lamb Lies Down on Broadway"1 terabyte El disco duro de consumo más grande en 2007
Video 1080p 4:3 de la serie de televisión animada "Avatar: The Last Airbender", los 61 episodios1 petabyte 2000 años de música codificada en MP3 1 exabyte Tráfico mensual global de Internet en 2004 1 zettabyte Tráfico anual global de Internet en 2016 Tabla 1: Equivalencias entre bytes y objetos reales Bases numéricas
Son un conjunto de reglas y símbolos utilizados para representar y contar cantidades en forma de números. Estas cantidades se pueden expresar mediante combinaciones de símbolos, y cada símbolo tiene un valor específico asociado.
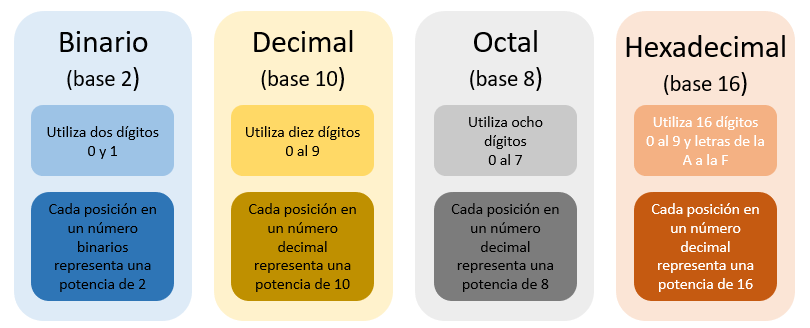
Figura 1: Sistemas numéricos -
Equivalencias entre bases numéricas
En la siguiente tabla puedes observar las equivalencias de los números del 0 al 15 en los distintos sistemas numéricos.
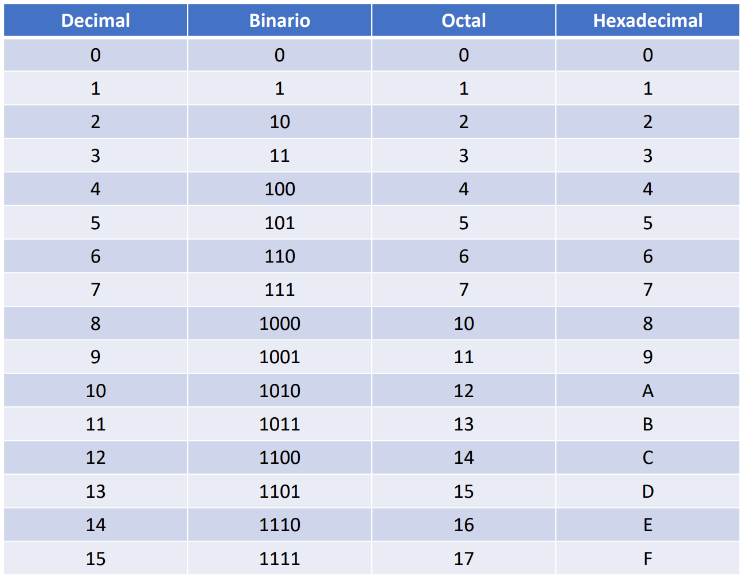
Figura 2: Equivalencias entre bases numéricas Convertir desde el sistema numérico decimal hacia cada uno de los otros sistemas
Vamos a transformar el número 35 de base decimal a binario.
- Se divide sucesivamente la cantidad decimal entre la base del sistema al cual se quiere convertir dicha cantidad (en este caso, 2 para el sistema binario).
- De cada división entera, anota el residuo.
- Toma los residuos en orden inverso, comenzando por el último cociente.
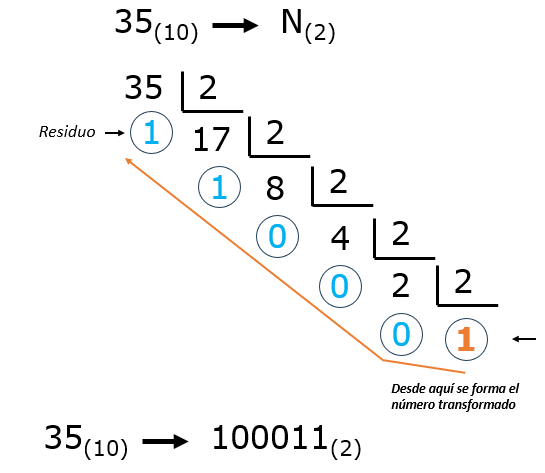
Figura 3: Ejemplo Conversión de base decimal a base binaria Veamos otro ejemplo: ahora queremos transformar el número 334 de base decimal a octal.
- Se divide sucesivamente la cantidad decimal para 8, que es la base del sistema octal.
- Anota el residuo de cada división entera.
- Toma los residuos en orden inverso, comenzando por el último cociente.
De esta forma, podemos transformar cualquier número de base decimal a otra base numérica.
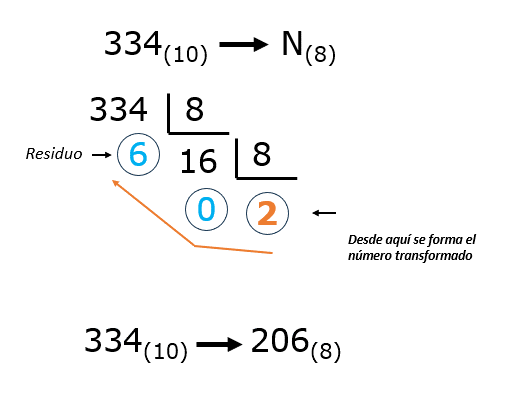
Figura 4: Ejemplo Conversión de base decimal a base octal -
Transformemos el número 1034 de base decimal a hexadecimal.
Recuerda que en el sistema hexadecimal se utilizan los números del 0 al 9 y las letras de la A a la F.
- Divide sucesivamente la cantidad decimal entre 16, que es la base del sistema hexadecimal.
- Anota el residuo de cada división entera.
- Toma los residuos en orden inverso, comenzando por el último cociente.
- En el caso de este ejemplo, el último residuo es 10, que equivale a la letra A en hexadecimal, por lo que el número hexadecimal resultante es 40A.
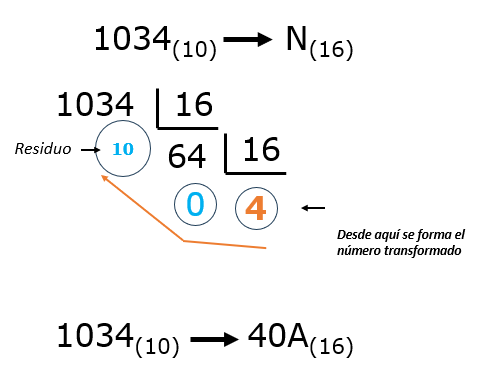
Figura 5: Ejemplo Conversión de base decimal a base octal Cómo convertir desde cada uno de los sistemas numéricos hacia el decimal
Para convertir un número de base N a base 10 (decimal), seguimos estos pasos:
- Toma el número que quieres transformar y, desde la derecha hacia la izquierda, asigna a cada dígito su valor correspondiente en la base que te han dado.
- Luego, multiplica cada dígito por el valor correspondiente, que es la potencia de la base N según la posición del dígito (empezando desde 0 en la derecha).
- Suma todos los resultados de las multiplicaciones. El resultado será el número en base 10 (decimal).
Ejemplo: Vamos a transformar un número de binario a decimal.
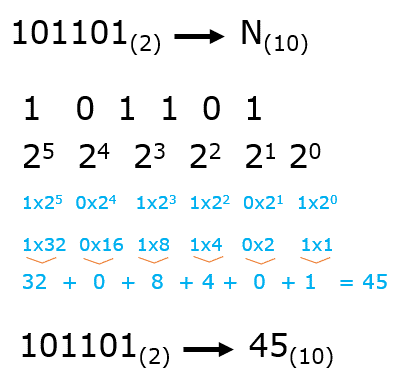
Figura 6: Ejemplos Conversión de base binaria a base decimal Observa otro ejemplo se va a transformar de base 8 a base 10 (decimal).
- Toma el número que quieres transformar y, desde la derecha hacia la izquierda, asigna a cada dígito su valor correspondiente en la base octal.
- Luego, multiplica cada dígito por su valor correspondiente.
- Suma todos los resultados de las multiplicaciones. El resultado será el número en base 10 (decimal).
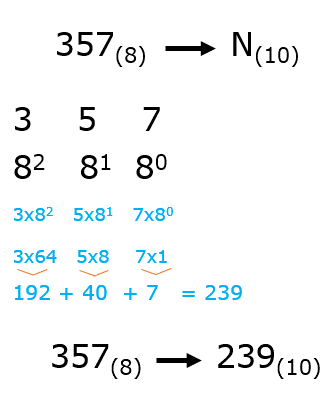
Figura 7: Ejemplos Conversión de base octal a base decimal Convertir desde el sistema binario a octal o hexadecimal y viceversa
- Encuentra la relación que existe entre la base 2 y la base resultante. Ejemplo:
- Base 2 a base 8 la relación (R) es 3 porque 23 = 8
- Base 2 a base Hexadecimal, R = 4 porque 24 = 16
- Separa los dígitos binarios en grupos de R (la relación) desde la derecha hacia la izquierda.
- Asigna a cada grupo un valor en la base resultante:
- Si es a base octal los números son 1,2, 4
- Si es a base hexadecimal, los números son 1, 2, 4, 8
- Calcula el valor de cada grupo sumando los bits que son "1" y tomando en cuenta solo esos unos.
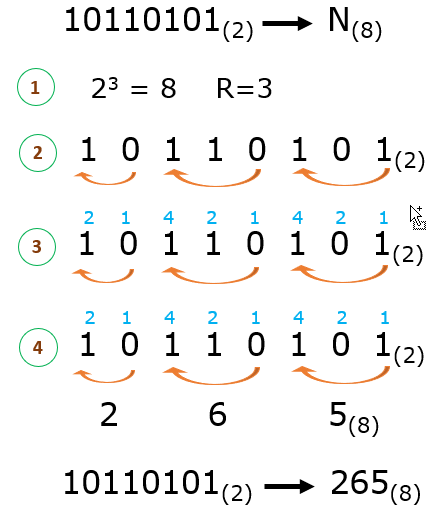
Figura 8: Ejemplo Conversión de base 2 a base 8 -
Make a submission
-
Magnitudes de datos