Interpretar datos trasciende la mera descripción estadística; significa tejer un puente entre números y narrativa, conectando resultados con su contexto más amplio. El análisis verdadero comienza donde terminan las cifras, integrando hallazgos en el marco conceptual, metodológico y teórico de la investigación. Analizar críticamente requiere ir más allá de lo superficial. Como sugieren Pérez y García (2023), ningún dato debe tomarse como verdad absoluta. El investigador debe examinar cada fase del proceso con mirada escéptica, reconociendo que su propia perspectiva inevitable e inconscientemente permea la interpretación, sin por ello renunciar a la rigurosidad científica.

20.1. Fundamentos del Pensamiento Crítico Aplicado a Datos

El pensamiento crítico exige desentrañar la génesis de los datos. Quienes investigan deben interrogar profundamente su origen:

• La procedencia: ¿Quién los recolectó? ¿Cuál fue su motivación real? La procedencia —ya sea empresarial, gubernamental, académica o individual— puede revelar sesgos ocultos que condicionan la interpretación. Cada fuente arrastra sus propias intenciones, que no siempre son neutrales. (Martínez, 2022).
• La rigurosidad metodológica: marca la diferencia entre datos confiables y meras especulaciones. Un investigador perspicaz examina críticamente cómo se seleccionó la muestra, identifica posibles distorsiones en el muestreo y evalúa la validez de los instrumentos de medición. La calidad de los resultados depende directamente de la solidez del proceso, más allá de análisis estadísticos sofisticados.
• El contexto —sea temporal, geográfico o social— resulta determinante para una interpretación precisa y matizada. Desentrañar el significado de los datos exige más que una simple lectura superficial. Los números cobran vida propia según cómo se definan sus variables: por ejemplo, ¿qué distingue realmente a un "empleado a tiempo completo"?
• Los sesgos pueden distorsionar cualquier análisis como un espejo deformante. El investigador debe estar alerta ante sesgos cognitivos —como el sesgo de confirmación—, metodológicos —selección o medición— e incluso en la presentación de resultados. Autores como Kahneman (2011) han destacado cómo estos prejuicios pueden alterar significativamente la comprensión de los datos. Tras cualquier conjunto de datos se esconden múltiples narrativas.
• Un pensamiento crítico riguroso implica explorar interpretaciones más allá de la propuesta inicial, desentrañando correlaciones que podrían malinterpretarse como causas directas. Como sugieren Pérez y García, la verdad rara vez se esconde en una única perspectiva.
• Evaluar la solidez de la evidencia requiere un análisis minucioso. ¿Son los datos lo suficientemente robustos para sustentar las conclusiones? El tamaño del efecto marca la diferencia entre lo trivial y lo sustantivo. Los intervalos de confianza revelan la incertidumbre subyacente. No toda observación equivale a evidencia científica rigurosa.

Aplicar pensamiento crítico a los datos constituye la primera línea de defensa contra el engaño estadístico. Un análisis agudo previene la incorporación acrítica de información que podría respaldar afirmaciones pseudocientíficas o generalizar indebidamente conocimientos empíricos limitados. La clave: mantener siempre una mirada escéptica pero constructiva. En la Figura 1 se identifican los elementos que se deben considerar al aplicar el pensamiento crítico al análisis de los datos

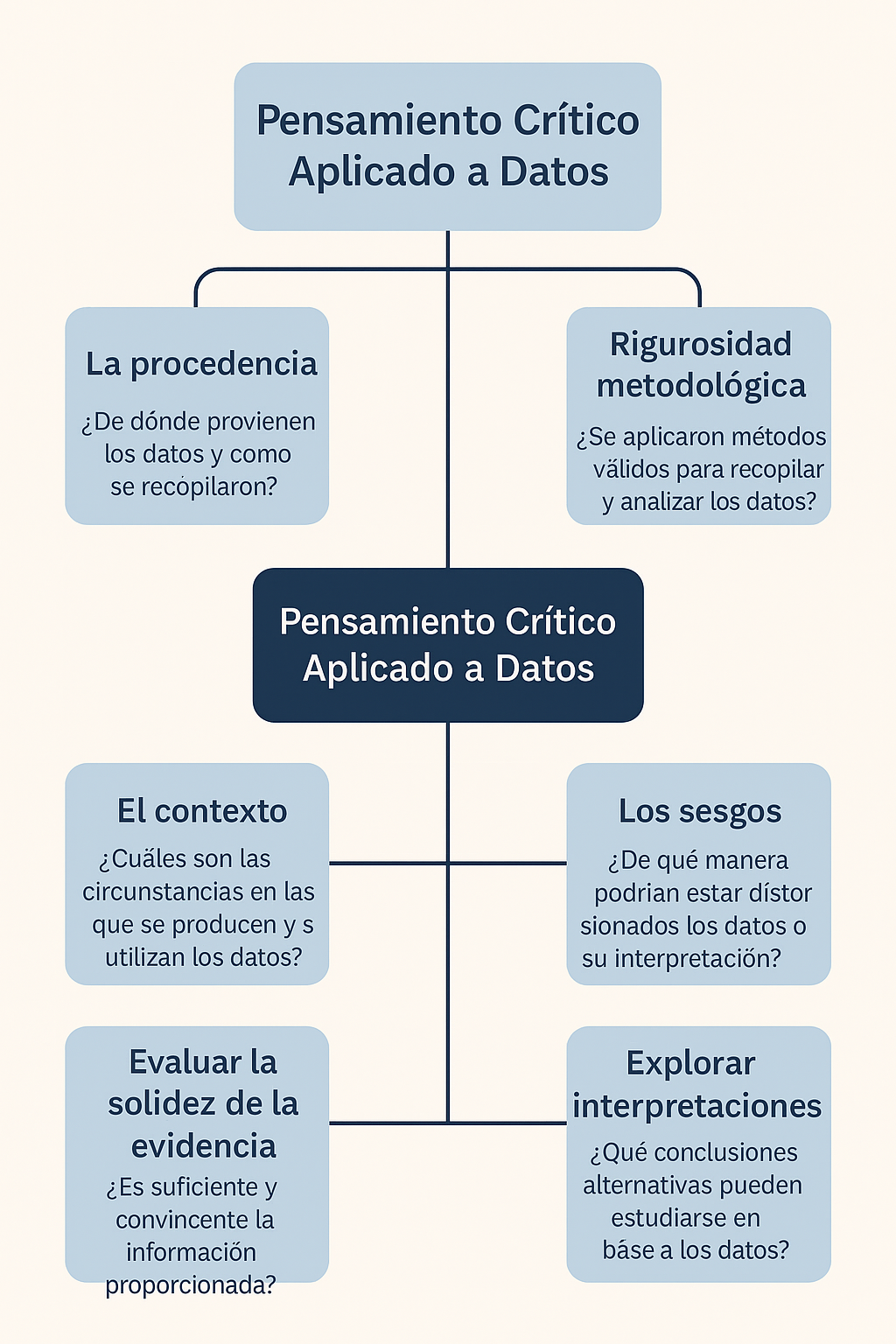
Figura 1: Elementos de pensamiento crítico aplicados al análisis de datos

×

Antes de sumergirse en el análisis de datos, es crucial comprender su esencia. Cada conjunto de información posee características únicas, y las variables se miden según diferentes escalas que condicionan la elección de técnicas estadísticas adecuadas y, consecuentemente, la interpretación de sus resultados (Pérez & García, 2023; Field, 2018).

Principalmente, los datos se clasifican en:

Datos Cualitativos (o Categóricos): Representan características o categorías que no tienen un valor numérico intrínseco que indique cantidad.

• Escala Nominal: Los números o etiquetas se usan solo para identificar o clasificar categorías, sin ningún orden implícito. No se pueden realizar operaciones matemáticas significativas con estos números.
• Ejemplo: Género (1=Masculino, 2=Femenino, 3=No binario), Nacionalidad, Estado civil, Tipo de red social (Facebook, Instagram, X). La interpretación se basa en frecuencias y proporciones (ej. "El 60% de los estudiantes usan Instagram").
• Escala Ordinal: Las categorías tienen un orden o rango, pero la distancia entre las categorías no es necesariamente igual o interpretable.
• Ejemplo: Nivel educativo (1=Primaria, 2=Secundaria, 3=Universidad), Nivel de acuerdo en una escala Likert (1=Totalmente en desacuerdo, ..., 5=Totalmente de acuerdo), Ranking de preferencia. La interpretación puede incluir la mediana, el rango intercuartílico, pero no la media o la desviación estándar de manera significativa como medida de tendencia o dispersión en la escala misma. Se interpretan posiciones relativas.

Datos Cuantitativos (o Numéricos): Representan cantidades y los números tienen un valor numérico real.

• Escala de Intervalo: Los datos tienen un orden y las distancias entre los puntos de datos son iguales y significativas, pero no hay un punto cero absoluto real (el cero no indica ausencia total de la característica). Se pueden calcular diferencias y promedios, pero no razones o proporciones significativas.
• Ejemplo: Temperatura en grados Celsius o Fahrenheit, Puntaje en un test estandarizado (donde un 0 no significa ausencia total de habilidad). Se interpretan diferencias y promedios (ej. "La temperatura promedio aumentó 5 grados").
• Escala de Razón: Similar a la escala de intervalo, pero con un punto cero absoluto real (el cero significa ausencia total de la característica). Se pueden realizar todas las operaciones matemáticas, incluyendo razones y proporciones significativas.
• Ejemplo: Edad, Peso, Altura, Número de hijos, Tiempo de uso de redes sociales por día (en minutos), Ingreso anual. Se interpreta la magnitud, diferencia, promedio, razón (ej. "El Grupo A pasó el doble de tiempo en redes sociales que el Grupo B").

En la Figura 2 se identifica la distribución de los datos de acuerdo con su tipología.

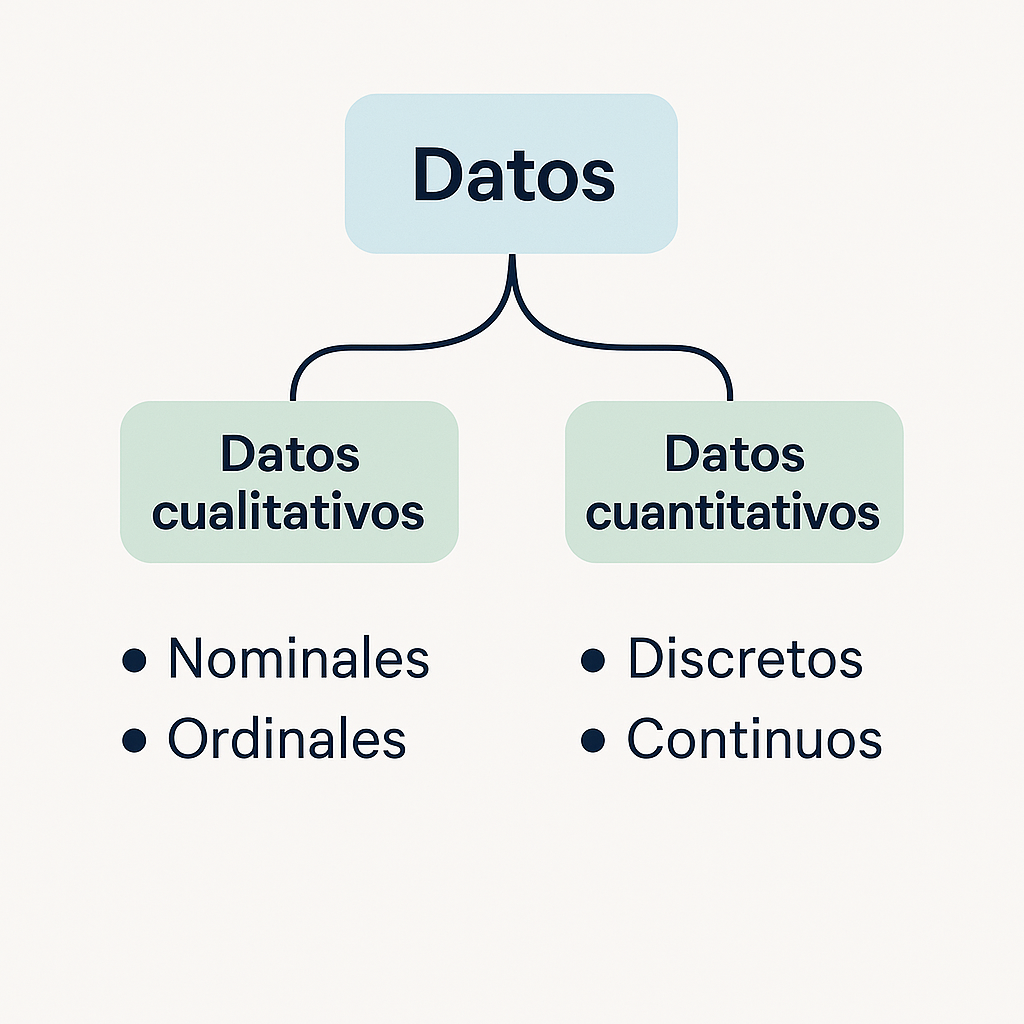
Figura 2: Tipología de datos
Gráfico generado con inteligencia artificial mediante Chat GPT (OpenAI) a partir de una descripción textual proporcionada por el autor.

×

La correcta identificación del tipo de datos y la escala de medición es el primer paso crítico en la interpretación. Intentar calcular un promedio para datos nominales o interpretar proporciones para datos de intervalo es un error conceptual básico que lleva a interpretaciones sin sentido, que podrían ser usadas para respaldar afirmaciones pseudocientíficas bajo una falsa apariencia de análisis cuantitativo.

Las estadísticas son las herramientas principales para resumir, analizar e interpretar datos cuantitativos. Se dividen en dos ramas principales:

Estadística Descriptiva:

• Propósito: Organizar, resumir y presentar características principales de un conjunto de datos de manera comprensible (Pérez & García, 2023). Describe lo que es el conjunto de datos estudiado.
• Medidas Clave:
• Medidas de Tendencia Central: Representan un valor típico o central del conjunto de datos. La elección depende de la escala de medición y la distribución de los datos.
• Media (Promedio): Suma de todos los valores dividida por el número de valores (para datos de intervalo/razón, preferiblemente sin valores atípicos extremos).
• Mediana: El valor central en un conjunto de datos ordenado (útil para datos ordinales o cuantitativos con distribución asimétrica o valores atípicos).
• Moda: El valor que ocurre con mayor frecuencia (útil para cualquier escala, especialmente nominal).
• Ejemplo: Si analizamos las horas de estudio semanales reportadas por 20 estudiantes, la media, mediana y moda nos darán una idea del tiempo de estudio "típico" en esa muestra.

Figura 3: Medidad de tendencia central
Gráfico generado con inteligencia artificial mediante Chat GPT (OpenAI) a partir de una descripción textual proporcionada por el autor.

×

En la Figura 3 se presenta un resumen de las medidas de tendencia central

• Medidas de Dispersión (o Variabilidad): Describen cuán dispersos o variados están los datos.
• Rango: Diferencia entre el valor máximo y mínimo.
• Varianza y Desviación Estándar: Miden la dispersión promedio de los datos respecto a la media (para datos de intervalo/razón). Una desviación estándar grande indica que los datos están muy dispersos.
• Rango Intercuartílico (RIC): La diferencia entre el tercer y el primer cuartil (útil con la mediana para datos ordinales o cuantitativos asimétricos).
• Ejemplo: Saber que el tiempo promedio de estudio es 15 horas no es suficiente; la desviación estándar nos dice si la mayoría estudia cerca de 15 horas (baja desviación) o si hay una gran variación (unos estudian muy poco y otros mucho, alta desviación).

En la Figura 4 se identifica un resumen con las medidas de dispersión

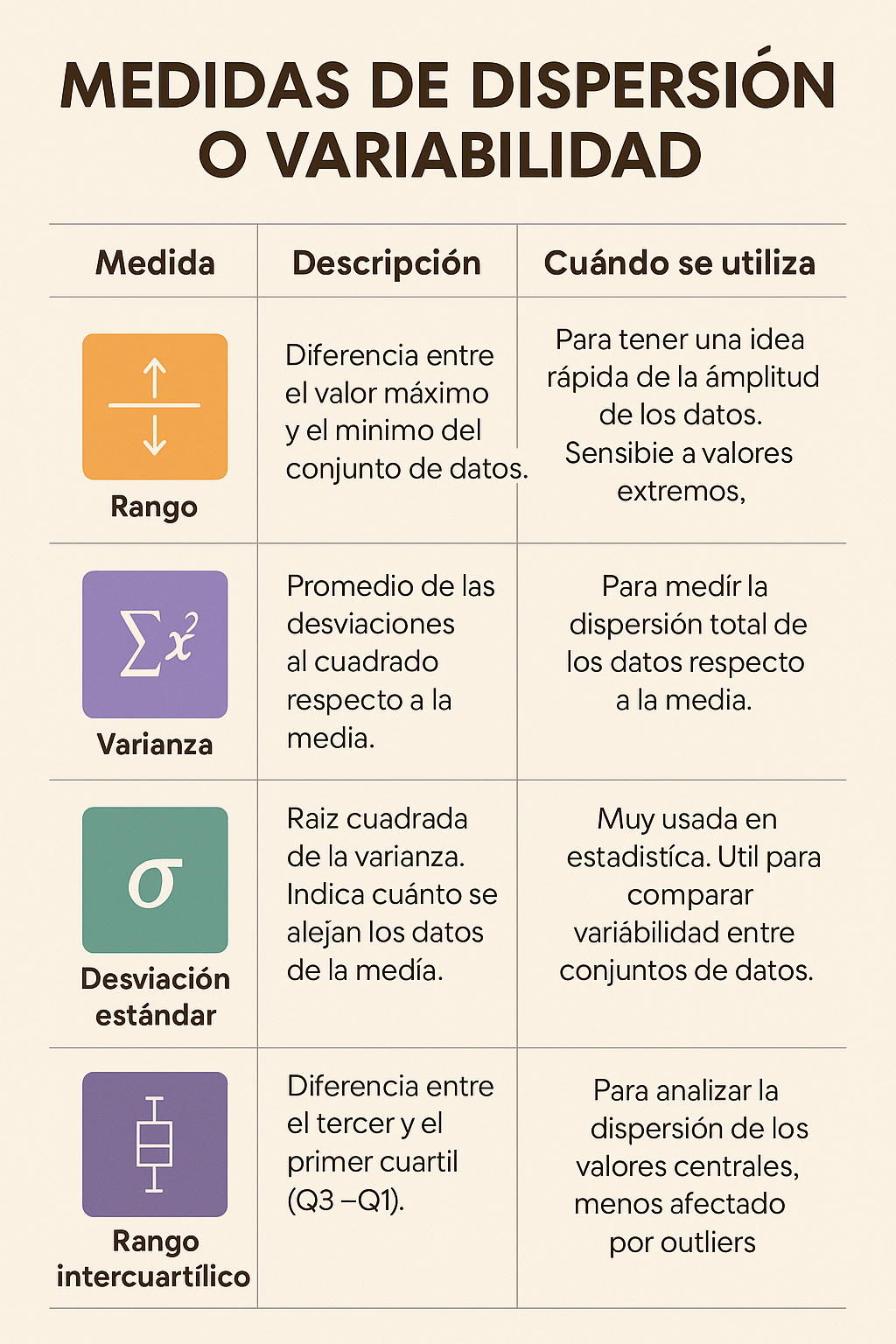
Figura 4: Medidas de dispersion
Nota. Gráfico generado con inteligencia artificial mediante Chat GPT (OpenAI) a partir de una descripción textual proporcionada por el autor.

×

• Distribuciones de Frecuencia: Tablas o gráficos que muestran cuántas veces ocurre cada valor o categoría en el conjunto de datos.
• La estadística descriptiva nos ayuda a resumir el conocimiento empírico recolectado en una muestra. Es el primer paso para darle sentido a los datos, pero no permite sacar conclusiones sobre una población más amplia o establecer causalidad.

Estadística Inferencial:

• Propósito: Utilizar datos de una muestra para hacer inferencias o generalizaciones sobre una población de la cual se extrajo la muestra (Martínez, 2022). Busca probar hipótesis y determinar la probabilidad de que los resultados observados se deban al azar.

Conceptos Clave:

• Población vs. Muestra: La población es el grupo total de interés (ej. todos los estudiantes universitarios de un país); la muestra es un subconjunto de la población que se estudia realmente.
• Prueba de Hipótesis: Procedimiento formal para decidir si los datos de la muestra proporcionan suficiente evidencia para rechazar una hipótesis nula preestablecida en favor de una hipótesis alternativa (Pérez & García, 2023).
• p-valor: La probabilidad de obtener los resultados observados (o resultados más extremos) si la hipótesis nula fuera cierta en la población. Un p-valor pequeño (típicamente ≤0.05) sugiere que los resultados son inusuales bajo la hipótesis nula, llevando a su rechazo.
• Intervalos de Confianza (IC): Un rango de valores dentro del cual se estima que se encuentra el verdadero parámetro de la población (ej. la media poblacional), con un cierto nivel de confianza (comúnmente 95%). Proporcionan una medida de la precisión de la estimación. Un IC amplio indica mayor incertidumbre.
• Tamaño del Efecto: Mide la magnitud o fuerza de la relación o diferencia observada, independientemente del tamaño de la muestra (Field, 2018; Martínez, 2022). Es crucial para evaluar la relevancia práctica de un resultado, distinguiéndola de la mera significancia estadística.
• Ejemplo: Queremos saber si un nuevo método de estudio mejora las calificaciones de todos los estudiantes universitarios. Estudiamos una muestra de 100 estudiantes. Usamos estadística inferencial (ej. prueba t) para comparar las calificaciones del grupo con el nuevo método y un grupo control. Un p-valor < 0.05 nos diría que la diferencia observada en la muestra es probablemente real y no solo casualidad, permitiéndonos inferir que el método probablemente tiene un efecto en la población. El tamaño del efecto nos diría cuán grande es esa mejora, ayudándonos a juzgar si es prácticamente relevante.

La inferencia estadística permite a los investigadores trascender la mera descripción de datos muestrales, adentrándose en conclusiones científicas sobre poblaciones enteras. No obstante, cada paso de este proceso depende crucialmente de la calidad metodológica: una muestra sesgada puede conducir a interpretaciones erróneas. Por ejemplo, un resultado con significancia estadística no garantiza relevancia práctica si su magnitud es insignificante o su intervalo de confianza resulta demasiado amplio, lo cual ocurre frecuentemente en publicaciones que buscan impresionar más que informar.

22.1. Creación e Interpretación de Visualizaciones de Datos

Las visualizaciones de datos (gráficos, tablas) son herramientas poderosas para comunicar hallazgos complejos de manera accesible y para explorar patrones en los datos. Sin embargo, también son una fuente frecuente de malentendidos y manipulación (Gómez, 2022).

• Propósito de la Visualización: Facilitar la comprensión, destacar tendencias, identificar patrones, comparar grupos y comunicar resultados de manera efectiva.
• Principios de una Buena Visualización: Claridad, precisión, honestidad, evitar la distorsión, elegir el tipo de gráfico adecuado para el tipo de datos y la pregunta de investigación (ej. barras para nominal/ordinal, histogramas para distribución de cuantitativas, dispersión para relación entre cuantitativas). El diseño debe servir al dato, no a la estética llamativa que pueda engañar.

En la Figura 5 se consolidan los elementos que se deben tomar en cuenta para lograr una buena visualización

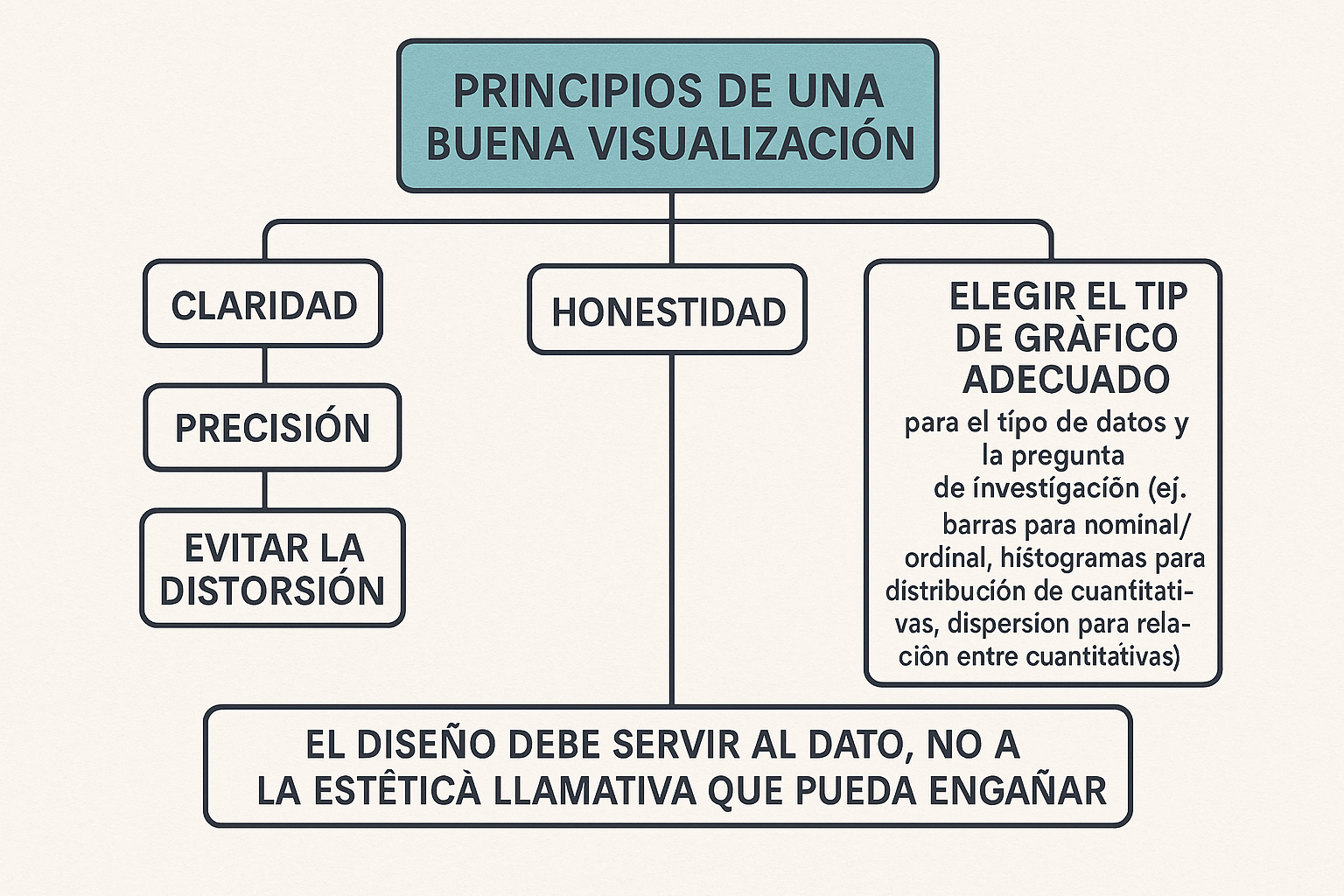
Nombre_de_la_figura

×

Figura 5: Elementos para una buena visualización
Nota. Gráfico generado con inteligencia artificial mediante Chat GPT (OpenAI) a partir de una descripción textual proporcionada por el autor. 

• Interpretación Crítica de Visualizaciones:
• Siempre leer los títulos, subtítulos, etiquetas de ejes y la leyenda. ¿Son claros? ¿Representan fielmente los datos?
• Examinar las escalas de los ejes. ¿El eje Y comienza en cero? ¿Las escalas son proporcionales? (Gómez, 2022).
• Considerar el tipo de gráfico. ¿Es apropiado para los datos y lo que se quiere mostrar?
• Buscar el contexto y la fuente de los datos. ¿Faltan datos? ¿Se excluyó un periodo de tiempo relevante?

En la Figura 6 se despliega el flujo que se debe tener para la interpretación crítica de las visualizaciones

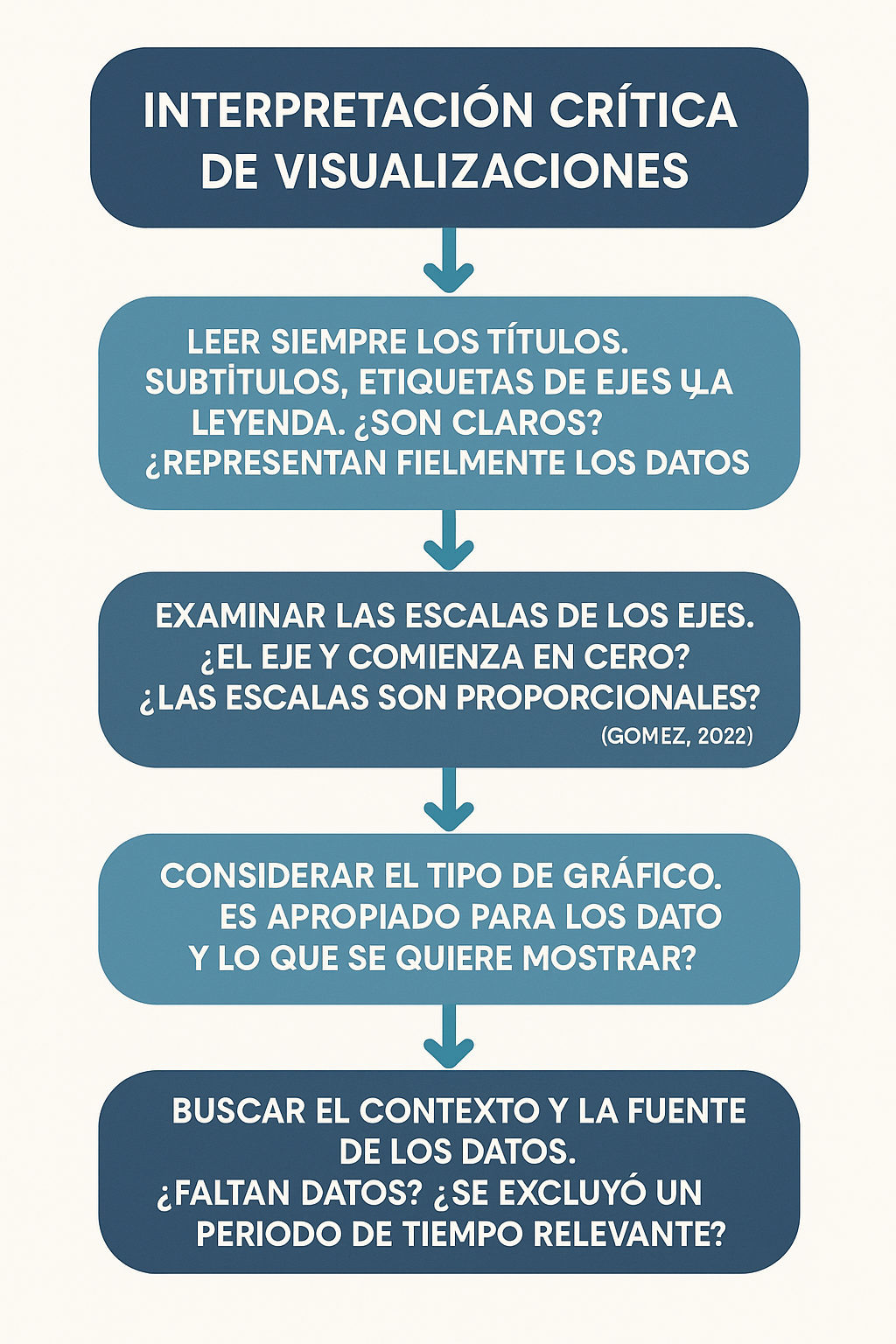
Figura 6: Flujo para interpretación critica de visualizaciones
Nota. Gráfico generado con inteligencia artificial mediante Chat GPT (OpenAI) a partir de una descripción textual proporcionada por el autor.

×

• Identificación de Visualizaciones Engañosas:
• Eje Y Truncado: Comienza el eje vertical por encima de cero para exagerar pequeñas diferencias (Gómez, 2022).
• Escalas Inconsistentes o Roturas de Eje: Distorsionan visualmente la magnitud de los cambios o diferencias.
• Gráficos 3D o con Efectos Decorativos: A menudo distorsionan las proporciones y dificultan la lectura precisa.
• Uso de Áreas o Volúmenes Desproporcionados: En pictogramas, escalar el alto y el ancho (o profundidad) de un ícono en proporción al valor hace que las diferencias grandes parezcan enormes.
• Selección de Periodos o Rangos de Datos Sesgados: Mostrar solo los datos que apoyan un argumento, ocultando la imagen completa.

La creación y lectura críticas de visualizaciones son habilidades de alfabetización de datos esenciales. Una gráfica engañosa puede hacer que el conocimiento empírico (los datos brutos) parezca respaldar una afirmación pseudocientífica o una conclusión estadística débil, simplemente manipulando la percepción visual (Gómez, 2022; Martínez, 2022).

22.2. Práctica: Análisis Crítico de Datos con Apoyo de IA

Las herramientas de inteligencia artificial se han convertido en aliadas potentes para desentrañar datos complejos, desde su limpieza inicial hasta la detección de patrones sutiles. No obstante, quien las utiliza debe mantener un ojo crítico: estas tecnologías pueden generar resultados que parecen científicos, pero esconden sesgos o narrativas engañosas provenientes de sus propios algoritmos de entrenamiento.

Cómo la IA Puede Apoyar el Análisis de Datos:

• Procesamiento y Limpieza de Datos: Ayudar a identificar errores, valores atípicos o datos faltantes.
• Generación de Código: Escribir código para análisis estadísticos o visualizaciones en software como R o Python.
• Identificación de Patrones: Explorar grandes conjuntos de datos para encontrar correlaciones o agrupaciones que podrían no ser obvias de inmediato.
• Generación de Visualizaciones: Crear gráficos basados en datos proporcionados.
• Resumen de Resultados Preliminares: Sintetizar los hallazgos estadísticos iniciales.

En la Figura 7 se identifica la manera en la que la Inteligencia Artificial puede apoyar al análisis de datos

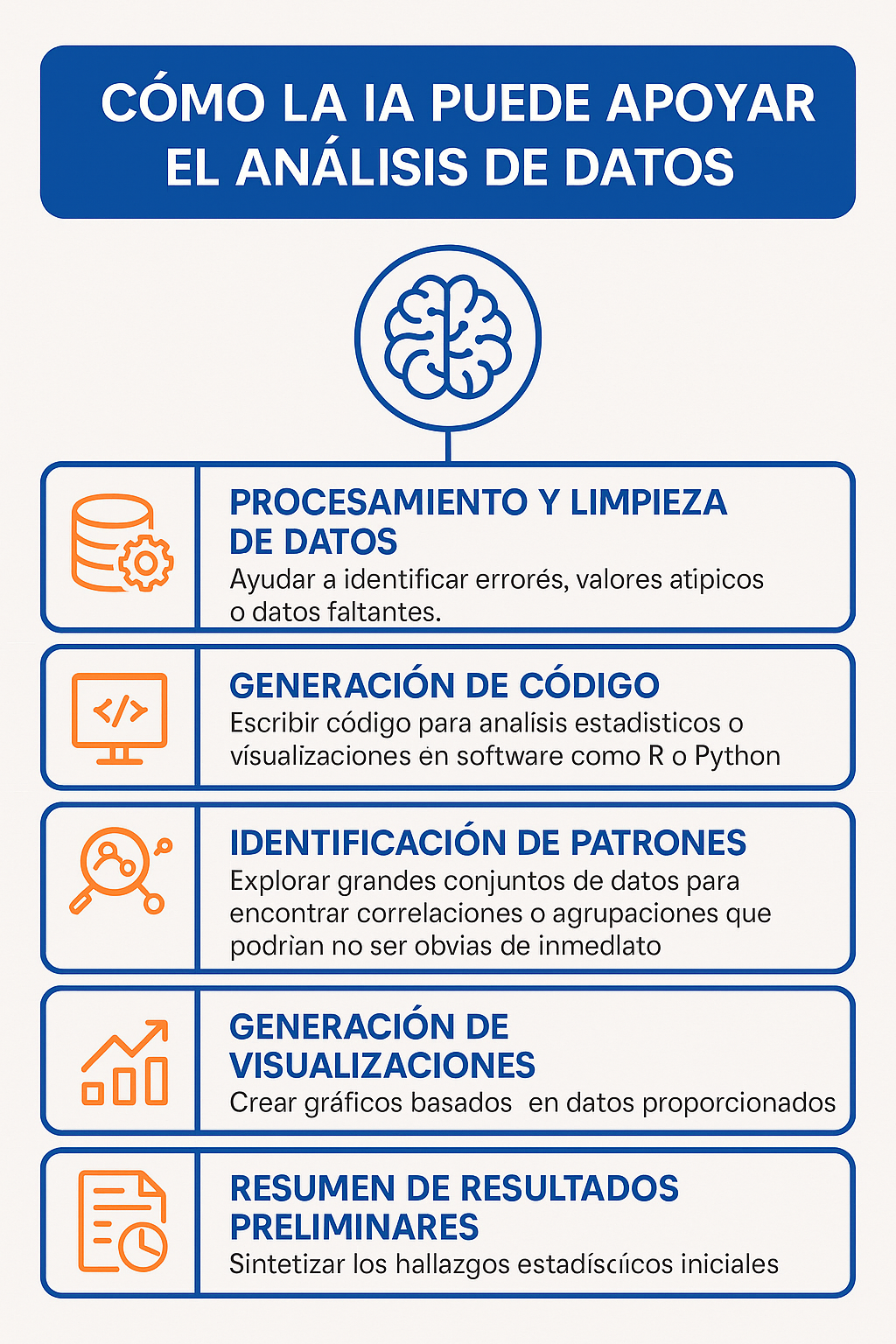
Figura 7: Apoyo de la IA en el análisis de datos
Nota. Gráfico generado con inteligencia artificial mediante Chat GPT (OpenAI) a partir de una descripción textual proporcionada por el autor.

×

Riesgos Críticos al Usar IA para Interpretar Datos:

• Generación de Interpretaciones Falaces: La IA puede identificar una correlación y redactar un texto que suena convincente, pero implica causalidad, sin base metodológica. Puede no entender el contexto o las limitaciones del diseño del estudio.
• Reproducción de Sesgos: Si los datos de entrenamiento o el prompt inicial contienen sesgos (ej. datos históricos con discriminación, prompts que dirigen la interpretación), la IA puede generar análisis o interpretaciones sesgadas.
• Creación de Visualizaciones Engañosas: Aunque la IA puede generar código para gráficos, sin instrucciones críticas explícitas, podría generar gráficos que utilicen ejes truncados o escalas inapropiadas si ha aprendido estos patrones de fuentes no rigurosas.
• Mezcla de Conocimiento: La IA no distingue inherentemente entre la interpretación de un ensayo controlado aleatorio (ciencia), una observación de cohorte (conocimiento empírico sistematizado), o una afirmación basada en anécdotas o pseudociencia (circulando en sus datos de entrenamiento). Puede fusionar interpretaciones de estas fuentes, creando un resultado plausible pero inválido.
• "Alucinaciones" Estadísticas: Puede inventar hallazgos, estadísticas o referencias a estudios que no existen.

La Práctica del Análisis Crítico con Apoyo de IA:

• El Humano es el Metodólogo y el Intérprete Final: La IA es una herramienta, no el investigador. El humano debe definir la pregunta, diseñar la metodología, seleccionar los datos apropiados y, crucialmente, supervisar y validar cada paso del análisis y la interpretación.
• Validar el Código y los Resultados Crudos: Si la IA genera código para un análisis, el investigador debe entender ese código y verificar que los resultados estadísticos brutos producidos sean correctos.
• Evaluar Críticamente las Interpretaciones Sugeridas: Si la IA ofrece una interpretación de los resultados ("los datos sugieren que A causa B"), el investigador debe aplicar todos los principios de pensamiento crítico: ¿Está metodológicamente justificada esa interpretación (ej. ¿es un diseño experimental o solo correlacional)? ¿La magnitud del efecto es relevante? ¿Hay explicaciones alternativas? ¿Es consistente con la literatura científica existente?
• Auditar las Visualizaciones Generadas: Revisar meticulosamente cada gráfico creado por IA, verificando ejes, escalas, títulos y asegurarse de que no inducen a error.
• Contrastar con Fuentes Fiables: Si la IA resume hallazgos o interpreta datos, verificar esas afirmaciones contrastándolas con la literatura científica revisada por pares, no con información genérica de internet (donde abunda la pseudociencia y el conocimiento empírico no validado).

El uso de IA para el análisis e interpretación de datos exige un nivel más alto de pensamiento crítico, no menor. Es una herramienta potente que, mal utilizada o sin la supervisión experta y crítica, puede generar rápidamente análisis e interpretaciones que parezcan ciencia pero que en realidad sean una amalgama de datos empíricos mal interpretados, sesgos y elementos pseudocientíficos aprendidos de su vasto pero desordenado corpus de entrenamiento. La distinción entre ciencia, pseudociencia y conocimiento empírico, por lo tanto, se vuelve no solo un ejercicio teórico, sino una habilidad práctica indispensable en la interpretación de datos con apoyo de IA para garantizar la integridad del conocimiento académico y científico.